Question

6．如图，△ABC中，∠BAC=90°AB=6，AC=8，在△ABC左边有一边长为4正方形从B点开始沿直线BC方向移动，直到不再与△ABC有重叠结束，若设平移的距离为t，正方形与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．

Answer 1

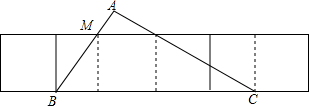
分析 自变量分6个区间讨论：①0＜t≤3，②3＜t≤4，③4＜t≤$\frac{14}{3}$，④$\frac{14}{3}$＜t≤7，⑤7＜t≤10，⑥10＜t≤14，根据三角形面积公式和梯形的面积公式即可求解．

解答 解：①0＜t≤3，S=$\frac{1}{2}$t×$\frac{4}{3}$t=$\frac{2}{3}$t²；
②3＜t≤4，S=$\frac{1}{2}$（t-3+t）×4=4t-6；
③4＜t≤$\frac{14}{3}$，S=4×4-$\frac{1}{2}$[4-（t-3）]×$\frac{4}{3}$[4-（t-3）]=-$\frac{2}{3}$t²+$\frac{4}{3}$t-$\frac{50}{3}$；
④$\frac{14}{3}$＜t≤7，S=4×4-$\frac{1}{2}$（t-$\frac{14}{3}$）×$\frac{3}{4}$（t-$\frac{14}{3}$）=-$\frac{3}{8}$t²+$\frac{7}{2}$t-$\frac{47}{6}$；
⑤7＜t≤10，S=$\frac{1}{2}$[$\frac{3}{4}$（10-t）+$\frac{3}{4}$（10-t+4）]×4=36-3t；
⑥10＜t≤14，S=$\frac{1}{2}$[4-（t-10）]×$\frac{3}{4}$[4-（t-10）]=$\frac{3}{8}$（t-14）²．

点评 考查了动点问题的函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．注意分类思想的应用．