
【题目】已知∠AOB内部有3条射线OE、OC、OF
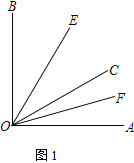
(1) 如图1,若∠AOB = 90°,∠AOC = 30°,OE平分∠BOC,OF平分∠AOC,求∠EOF的度数.
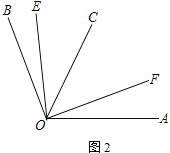
(2) 如图2,若∠AOB = α,∠EOB = ∠COB,∠COF = ∠FOA,求∠EOF的度数(用含α的式子表示)
【答案】(1)∠EOF=45°;(2)∠EOF=![]() α.
α.
【解析】
(1)首先根据角平分线的定义求得∠COF,然后求得∠BOC的度数,根据角平分线的定义求得∠EOC,然后根据∠EOF=∠COF+∠EOC求解;
(2)根据角平分线的定义可以得到∠COF=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,然后根据∠EOF=∠COF+∠EOC=
∠BOC,然后根据∠EOF=∠COF+∠EOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)即可得到.
(∠AOC+∠BOC)即可得到.
解:(1)∵OF平分∠AOC,
∴∠COF=![]() ∠AOC=
∠AOC=![]() ×30°=15°,
×30°=15°,
∵∠BOC=∠AOB-∠AOC=90°-30°=60°,OE平分∠BOC,
∴∠EOC=![]() ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠COF+∠EOC=45°;
(2)∵OF平分∠AOC,
∴∠COF=![]() ∠AOC,
∠AOC,
同理,∠EOC=![]() ∠BOC,
∠BOC,
∴∠EOF=∠COF+∠EOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB=
∠AOB=![]() α;
α;


科目:初中数学 来源: 题型:
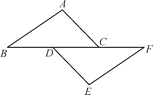
【题目】如图,点D,C在BF上,AC∥DE,∠A=∠E,BD=CF.
(1)求证:AB=EF;
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若一次函数![]() 的图象与x轴的交于点
的图象与x轴的交于点![]() ,与y轴交于点
,与y轴交于点![]() 下列结论:①关于x的方程
下列结论:①关于x的方程![]() 的解为
的解为![]() ;②
;②![]() 随x的增大而减小;③关于x的方程
随x的增大而减小;③关于x的方程![]() 的解为
的解为![]() ;④关于x的不等式
;④关于x的不等式![]() 的解为
的解为![]() 其中所有正确的为
其中所有正确的为![]()
![]()

A. ①②③ B. ①③ C. ①②④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为线段AD外一点,M、C、B、N为AD上任意四点,连接OM、OC、OB、ON,下列结论不正确的是( )
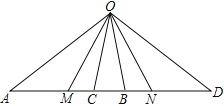
A. 以O为顶点的角共有15个
B. 若OM平分∠AOC,ON平分∠BOD,∠AOD=5∠COB,则∠MON=![]() (∠MOC+∠BON)
(∠MOC+∠BON)
C. 若M为AB中点,N为CD中点,则MN=![]() (AD-CB)
(AD-CB)
D. 若MC=CB,MN=ND,则CD=2CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC= ![]()

(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)所作的圆中,圆心角∠BOC=°,圆的半径为 , 劣弧 ![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.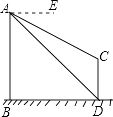
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
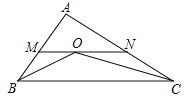
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )
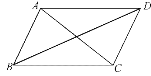
A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com