
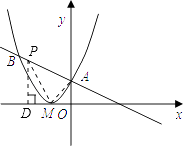
【题目】如图,已知直线y=﹣ ![]() x+2与抛物线y=a (x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a (x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
(1)请直接写出点A的坐标及该抛物线的解析式;
(2)若P为线段AB上一个动点(A、B两端点除外),连接PM,设线段PM的长为l,点P的横坐标为x,请求出l2与x之间的函数关系,并直接写出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在点P,使以A、M、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:A的坐标是(0,2),抛物线的解析式是y= ![]() (x+2)2.
(x+2)2.
联立直线与抛物线解析式可得B点坐标为(﹣5, ![]() )
)
(2)
解:如图,P为线段AB上任意一点,连接PM,
过点P作PD⊥x轴于点D,
设P的坐标是(x,﹣ ![]() x+2),则在Rt△PDM中,
x+2),则在Rt△PDM中,
PM2=DM2+PD2
即l2=(﹣2﹣x)2+(﹣ ![]() x+2)2=
x+2)2= ![]() x2+2x+8,
x2+2x+8,
P为线段AB上一个动点,故自变量x的取值范围为:﹣5<x<0,
答:l2与x之间的函数关系是l2= ![]() x2+2x+8,自变量x的取值范围是﹣5<x<0.
x2+2x+8,自变量x的取值范围是﹣5<x<0.
(3)
解:存在满足条件的点P,
连接AM,
由题意得,AM= ![]() =2
=2 ![]() ,
,
①当PM=PA时, ![]() x2+2x+8=x2+(﹣
x2+2x+8=x2+(﹣ ![]() x+2﹣2)2,
x+2﹣2)2,
解得:x=﹣4,
此时y=﹣ ![]() ×(﹣4)+2=4,
×(﹣4)+2=4,
∴点P1(﹣4,4);
②当PM=AM时, ![]() x2+2x+8=(2
x2+2x+8=(2 ![]() )2,
)2,
解得:x1=﹣ ![]() x2=0(舍去),
x2=0(舍去),
此时y=﹣ ![]() ×(﹣
×(﹣ ![]() )+2=
)+2= ![]() ,
,
∴点P2(﹣ ![]() ,
, ![]() ),
),
③当PA=AM时,x2+(﹣ ![]() x+2﹣2)2=(2
x+2﹣2)2=(2 ![]() )2,
)2,
解得:x1=﹣ ![]() x2=
x2= ![]() (舍去),
(舍去),
此时y=﹣ ![]() ×(﹣
×(﹣ ![]() )+2=
)+2= ![]() ,
,
∴点P3(﹣ ![]() ,
, ![]() ),
),
综上所述,满足条件的点为:
P1(﹣4,4)、P2(﹣ ![]() ,
, ![]() )、P3(﹣
)、P3(﹣ ![]() ,
, ![]() ),
),
答:存在点P,使以A、M、P为顶点的三角形是等腰三角形,点P的坐标是(﹣4,4)或(﹣ ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
【解析】(1)把x=0代入求出A的坐标,求出直线与抛物线的交点坐标即可;(2)过点P作PD⊥x轴于点D,设P的坐标是(x,﹣ ![]() x+2),根据勾股定理求出x即可;(3)连接AM,求出AM,①当PM=PA时,根据勾股定理得到
x+2),根据勾股定理求出x即可;(3)连接AM,求出AM,①当PM=PA时,根据勾股定理得到 ![]() x2+2x+8=x2+(﹣
x2+2x+8=x2+(﹣ ![]() x+2﹣2)2 , 求出方程的解即可;同理②当PM=AM时,求出P的坐标;③当PA=AM时,求出P的坐标.
x+2﹣2)2 , 求出方程的解即可;同理②当PM=AM时,求出P的坐标;③当PA=AM时,求出P的坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF. 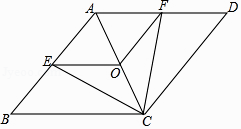
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7) 
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年入春以来,湖南省大部分地区发生了罕见的旱灾,连续几个月无有效降水.为抗旱救灾,驻湘某部计划为驻地村民新建水渠3600米,为使水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在完全相同的四张卡片上分别写有如下四个命题:①半圆所对的弦是直径;②圆既是轴对称图形,也是中心对称图形;③弦的垂线一定经过这条弦所在圆的圆心;④圆内接四边形的对角互补.把这四张卡片放入一个不透明的口袋内搅匀,从口袋内任取一张卡片,则取出卡片上的命题是真命题的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5. 月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线y= ![]() (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣ ![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形. 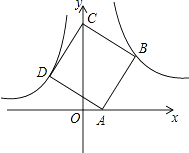
(1)求k的值;
(2)求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com