
【题目】如图,点P是∠AOB内任意一点,OP=5,M,N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为_____.

【答案】30°.
【解析】
如图:分别作点P关于OB、AO的对称点P'、P',分别连OP'、O P'、P' P'交OB、OA于M、N,则可证明此时△PMN周长的最小,由轴对称性,可证明△P'O P'为等边三角形,∠AOB=![]() ∠P'O P'=30°.
∠P'O P'=30°.
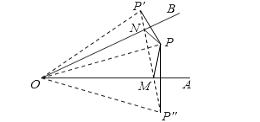
解:如图:分别作点P关于OB、AO的对称点P'、P',分别连OP'、O 、P' 交OB、OA于M、N,
由轴对称△PMN周长等于PN+NM+MP=P'N+NM+MP"=P'P"
∴由两点之间线段最短可知,此时△PMN周长的最小
∴P'P"=5
由对称OP=OP'=OP"=5
∴△P'OP"为等边三角形
∴∠P'OP"=60
∵∠P'OB=∠POB,∠P"OA=∠POA
∴∠AOB=![]() ∠P'O P'=30°.
∠P'O P'=30°.
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
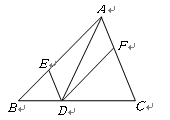
【题目】如图,在![]() 中,点D、E、F分别在边
中,点D、E、F分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列四种说法:
.下列四种说法:
①四边形![]() 是平行四边形;②如果
是平行四边形;②如果![]() ,那么四边形
,那么四边形![]() 是矩形;
是矩形;
③如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是菱形;
是菱形;
④如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.
是菱形.
其中,正确的有 .(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
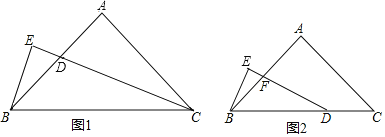
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
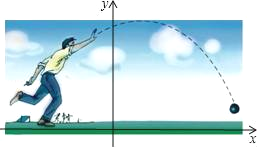
【题目】如图,一名男生推铅球,铅球行进的高度y(m)与水平距离x(m)之间的关系是二次函数的关系.铅球行进起点的高度为![]() m,行进到水平距离为4m时达到最高处,最大高度为3m.
m,行进到水平距离为4m时达到最高处,最大高度为3m.
(1)求二次函数的解析式(化成一般形式);
(2)求铅球推出的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点
的中点
情景引入:
(1)如图1,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,DC之间的等量关系.
,DC之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断
转化在一个三角形中即可判断![]() ,
,![]() ,
,![]() 之间的等量关系为
之间的等量关系为![]() ,试证明该结论;
,试证明该结论;

问题探究:
(2)如图2,点![]() 是
是![]() 的延长线上一点,连
的延长线上一点,连![]() ,若
,若![]() 恰好是
恰好是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
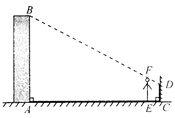
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com