
���� ��1�����ݡ�����200Ԫ������500Ԫ�İ�9���Żݡ��ɵã�200��90%=180Ԫ�����ڵ�һ�ι���134Ԫ��180Ԫ���ʲ������κ��Żݣ��ɡ�����500Ԫ������500Ԫ��9���Żݣ���������8���Żݡ���֪500��90%=450Ԫ��482��450Ԫ���ʴ��˹������ܡ�����500Ԫ������500Ԫ��9���Żݣ���������8���Żݡ�������������ֵxԪ�Ļ����������500ԪǮʱ��9���Żݣ������ܳ���500Ԫ��8���Żݣ������εĻ��Ѽ����������������˵ڶ��ι��ﲻ���۵Ļ��ѣ�
��2����ʡ��Ǯ��=�����ۻ���-ʵ�ʽ��ѣ�
��3���������ι���IJ����۵�����-500Ԫ����80%+500��90%����������ι����Ϊһ�ι���ʵ��Ӧ�����ã����������ι��������ķ��ý��бȽϼ��ɣ�
��� �⣺��1������Ϊ134Ԫ��200��90%=180Ԫ�����Ը��˲������Żݣ�
����Ϊ�ڶ��θ���482Ԫ��500��90%=450Ԫ�����Ը������ܳ���500Ԫ������500Ԫ��9���Żݣ���������8���Żݣ�
����������ֵxԪ�Ļ��
��90%��500+��x-500����80%=482��
���x=540��
540+134=674��Ԫ����
�𣺴������ι�������Ʒ������ֵ674ԪǮ��
��2��540-482=58��Ԫ����
������λ������ʡ��58ԪǮ��
��3��500��90%+��674-500����80%=589.2��Ԫ����
134+482=616��Ԫ����
��589.2��616��
����˽������ι����Ϊһ�ι������ʡ��
���� ������Ҫ������ʵ�������е��ۿ����⣬�ؼ������÷������۵�˼�룺�������������۵����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10070 | B�� | 10071 | C�� | 10095 | D�� | 10097 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
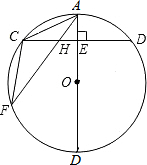 ��ͼ��ABΪ��O��ֱ������CD��AB�ڵ�E����F�ǡ�O��һ�㣬����AC��AF��CF����֤����ACH�ס�AFC��
��ͼ��ABΪ��O��ֱ������CD��AB�ڵ�E����F�ǡ�O��һ�㣬����AC��AF��CF����֤����ACH�ס�AFC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
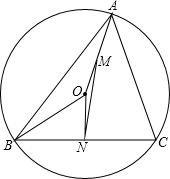 ��ͼ����֪��ǡ�ABC������ΪO���߶�OA��BC���е�ֱ�Ϊ��M��N������OBN=2��OMN��$\widehat{AC}$�Ķ���Ϊ90�㣬���OMN�Ĵ�С��
��ͼ����֪��ǡ�ABC������ΪO���߶�OA��BC���е�ֱ�Ϊ��M��N������OBN=2��OMN��$\widehat{AC}$�Ķ���Ϊ90�㣬���OMN�Ĵ�С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
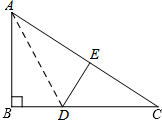 ��ͼ����Rt��ABC�У���ABC=90�㣬AC=10��BC=8��AD�ǡ�BAC��ƽ���ߣ���E��б��AC�ϵ�һ�㣬��AE=AB���ء�DEC��һ���ڽ�ƽ�����۵���ʹ��C����DE����ֱ���ϣ����ۺ۵ij���Ϊ$\frac{12\sqrt{2}}{7}$��$\frac{3\sqrt{5}}{2}$��
��ͼ����Rt��ABC�У���ABC=90�㣬AC=10��BC=8��AD�ǡ�BAC��ƽ���ߣ���E��б��AC�ϵ�һ�㣬��AE=AB���ء�DEC��һ���ڽ�ƽ�����۵���ʹ��C����DE����ֱ���ϣ����ۺ۵ij���Ϊ$\frac{12\sqrt{2}}{7}$��$\frac{3\sqrt{5}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com