
【题目】在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )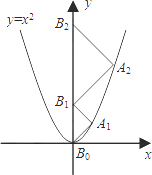
A.2013
B.2014
C.2013 ![]()
D.2014 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )

A.18B.20C.22D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
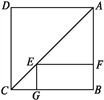
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
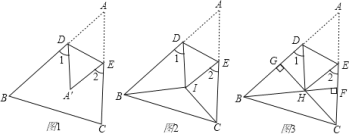
【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,若∠A=50°,求∠1+∠2的度数,猜想并直接写出∠1+∠2与∠A的数量关系.(不必证明)
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=110°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com