

���� ��1������A��B���������߽���ʽ�����a��bֵ���ɵõ������߽���ʽ��
��2��������֪�����D�����꣬��y����ȡ��G��ʹGC=CD=2��ֻҪ֤��֤����CDB�ա�CGB����֪��PBC=��DBC��д��ֱ��BP����ʽ���������κ�������ʽ�������P���ꣻ
��3���������������һ������ص�����Ϊ�ı��Σ����ô������μ�ȥ����С��������ý���ʽ���ڶ�������ص�����Ϊ�����Σ������������������ʽ��ã�
��� �⣺��1����A��-1��0����B��3��0������������y=ax2+bx+3��a��0����
$\left\{\begin{array}{l}{9a+3b+3=0}\\{a-b+3=0}\end{array}\right.$��
��ã�a=-1��b=2��
�������߽���ʽΪ��y=-x2+2x+3��
��2������
����D���������߽���ʽ�ã�m=3��
��D��2��3����
��x=0��y=3��
��C��0��3����
��OC=OB��
���OCB=��CBO=45�㣬
����ͼ��
��y����ȡ��G��ʹGC=CD=2��
�ڡ�CDB���CGB��
��BC=BC����DCB=��BCO��GC=DC��SAS��
���CDB�ա�CGB��
���PBC=��DBC��
�ߵ�G��0��1����
��ֱ��BP��y=kx+1��
�����B��3��0����
��k=-$\frac{1}{3}$��
��ֱ��BP��y=-$\frac{1}{3}$x+1��
����ֱ��BP�Ͷ��κ�������ʽ��
$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-\frac{1}{3}x+1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{x}_{1}=-\frac{2}{3}}\\{{y}_{1}=\frac{11}{9}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=0}\end{array}\right.$���ᣩ��
��P��-$\frac{2}{3}$��$\frac{11}{9}$����
��3��ֱ��BC��y=-x+3��ֱ��BD��y=-3x+9��
��0��t��2ʱ������ͼ��
��ֱ��C��B�䣺y=-��x-t��+3
����ֱ��BD���F��$\frac{6-t}{2}$��$\frac{3t}{2}$����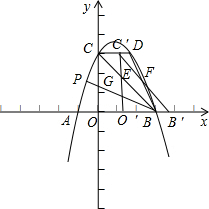
S=S��BCD-S��CC��E-S��C��DF
=$\frac{1}{2}$��2��3-$\frac{1}{2}$��t��t-$\frac{1}{2}$����2-t����3-$\frac{3t}{2}$��
�����ã�S=-$\frac{5}{4}$t2+3t��0��t��2����
��2��t��3ʱ������ͼ��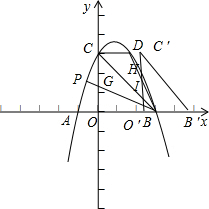
H��t��-3t+9����I��t��-t+3��
S=S��HIB=$\frac{1}{2}$[��-3t+9��-��-t+3��]����3-t��
�����ã�S=t2-6t+9��2��t��3��
����������S=$\left\{\begin{array}{l}{-\frac{5}{4}{t}^{2}+3t��0��t��2��}\\{{t}^{2}-6t+9��2��t��3��}\end{array}\right.$��
���� ��Ŀ������κ����ۺ�Ӧ�ã�ͨ���Զ��κ�����һ�κ�������ʽ����⣬��ϵ��������μ�ͼ�������⣬����ѧ���Ĺ۲����������ͽ�������������ر���ͼ���������⣬����ѧ��������������ߵ�Ҫ����Ŀ������ѣ��ʺ�ѧ�������п�ѹ����Ŀѵ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 10�� | B�� | 15�� | C�� | 20�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
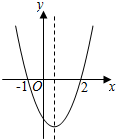 ���κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ�����ڸö��κ���������˵������ȷ���ǣ�������
���κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ�����ڸö��κ���������˵������ȷ���ǣ�������| A�� | �ú�������Сֵ | B�� | y��x����������� | ||
| C�� | �Գ�����ֱ��$x=\frac{1}{2}$ | D�� | ��-1��x��2ʱ��y����0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
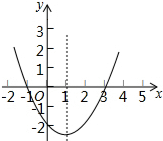 ���κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ�����ڸö��κ���������˵��������ǣ�������
���κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ�����ڸö��κ���������˵��������ǣ�������| A�� | ��������Сֵ | B�� | ��-1��x��3ʱ��y��0 | ||
| C�� | ��x��1ʱ��y��x���������С | D�� | �Գ�����ֱ��x=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��2�� | B�� | ��2��-1�� | C�� | ��1��2�� | D�� | ��-1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
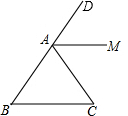 ��ͼ���ڡ�ABC�У�AB=AC��AM����ǡ�DAC��ƽ���ߣ�
��ͼ���ڡ�ABC�У�AB=AC��AM����ǡ�DAC��ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ʮ�˴������������ǿ����������������г���������ɡ�ƽ�ȡ����������Σ�������������ҵ�����š����ƣ����������ͼ������������ļ�ֵ�ۣ���24���������������ļ�ֵ�۵Ļ������ݣ����У�
����ʮ�˴������������ǿ����������������г���������ɡ�ƽ�ȡ����������Σ�������������ҵ�����š����ƣ����������ͼ������������ļ�ֵ�ۣ���24���������������ļ�ֵ�۵Ļ������ݣ����У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�BA=BC����ABC=120�㣬AB�Ĵ�ֱƽ������AC���ڵ�D������Ϊ��F����̽���߶�AD��DC��������ϵ����֤����Ľ��ۣ�
��ͼ���ڡ�ABC�У�BA=BC����ABC=120�㣬AB�Ĵ�ֱƽ������AC���ڵ�D������Ϊ��F����̽���߶�AD��DC��������ϵ����֤����Ľ��ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com