
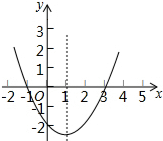 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 当-1<x<3时,y>0 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 对称轴是直线x=1 |
分析 由抛物线开口向上得函数有最小值;
观察函数图象得到当-1<x<3时,图象在x轴下方,则y<0;
根据二次函数的性质可得当x<1时,y随x的增大而减小;
根据抛物线的对称性可得到抛物线的对称轴为直线x=1.
解答 解:A、∵抛物线开口向上,
∴函数有最小值,故本选项正确;
B、当-1<x<3时,y<0,故本选项错误;
C、∵抛物线开口向上,
∴当x<1时,y随x的增大而减小,故本选项正确;
D、∵抛物线与x轴的交点坐标为(-1,0)、(3,0),
∴抛物线的对称轴为直线x=1,故本选项正确.
故选B.
点评 本题考查了二次函数的图象:y=ax2+bx+c的图象为抛物线,可利用列表、描点、连线画出二次函数的图象.也考查了二次函数的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
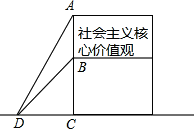 为了弘扬“社会主义核心价值观”,乐至县政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的距离分别是5米和$3\sqrt{2}$米.
为了弘扬“社会主义核心价值观”,乐至县政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的距离分别是5米和$3\sqrt{2}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8只 | B. | 12只 | C. | 18只 | D. | 30只 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.28×10-8米 | B. | 2.8×10-10米 | C. | 2.8×10-9米 | D. | 2.8×10-8米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com