Question

9．感知：如图①，分别以△ABC中AB，AC为边向外作正方形ABDE和正方形ACGF，点E，A，C不在同一条直线上，连接CE，BF，易证△ACE≌△AFB．（不要求证明）
拓展：如图②，分别以△ABC中AB，AC为边向外作△ABD和△ACE，使AD=AB，AE=AC，∠DAB=∠EAC，且点D，A，C不在同一条直线上，连接DC，BE，求证：△ACD≌△AEB．
应用：在图②中，分别取边EC，CB，BD的中点F，G，H，连接FG，GH，若∠FGH=132°，则∠ADB的大小为66度．

Answer 1

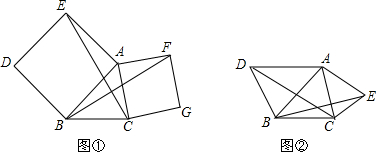
分析 感知：根据四边形ABDE和四边形ACGF是正方形，得到AE=AB，AF=AC，∠EAB=∠FAC，推出∠EAC=∠FAB，即可得到△ACE≌△AFB；
拓展：根据已知条件得到∠DAC=∠BAE，根据全等三角形的判定定理即可得到结论；
应用：如图②，设HG、BE交于Q，FG、CD交于P，CD、BE交于H，根据三角形的中位线得到HG∥CD，GF∥BE，证得四边形GPHQ是平行四边形，根据平行四边形的性质得到∠BHC=∠HGF=132°，于是得到∠DHB=180°-∠BHC=48°，根据全等三角形的性质得到∠ADC=∠ABE，推出D，B，H，A四点共圆，根据圆周角定理得到∠DAB=∠BHD=48°，根据等腰三角形的性质即可得到结论．

解答 感知：证明：∵四边形ABDE和四边形ACGF是正方形，
∴AE=AB，AF=AC，∠EAB=∠FAC，
∴∠EAC=∠FAB，
在△AEC与△FAB中，$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAF}\\{AC=AF}\end{array}\right.$，
∴△ACE≌△AFB；

拓展：证明：∵∠DAB=∠EAC，
∴∠DAC=∠BAE，
在△ADC与△ABE中，$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$，
∴△ACD≌△AEB；

应用：如图②，设HG、BE交于Q，FG、CD交于P，CD、BE交于H，
∵BH=DH，BG=CG，CF=EF，
∴HG∥CD，GF∥BE，
∴四边形GPHQ是平行四边形，
∴∠BHC=∠HGF=132°，
∴∠DHB=180°-∠BHC=48°，
∵△ACD≌△AEB，
∴∠ADC=∠ABE，
∴D，B，H，A四点共圆，
∴∠DAB=∠BHD=48°，
∵AD=AB，
∴$∠ADB=∠ABD=\frac{180°-∠DAB}{2}$=66°．
故答案为：66．

点评 本题考查了全等三角形的判定和性质，等腰三角形的性质，正方形的性质，三角形的中位线的性质，四点共圆，熟练掌握全等三角形的判定和性质是解题的关键．