
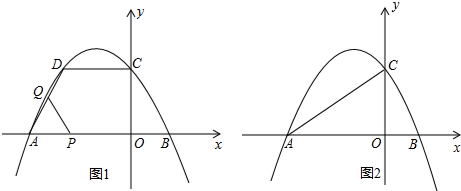
分析 (1)直接代入求得函数解析式即可,由点D与C对称求得点D坐标即可;
(2)由特殊角的三角函数值得出∠DAP=60°,则点Q一直在直线AD上运动,分别探讨当点P在线段AO上;点Q在AD的延长线上,点P在线段OB上以及点Q在AD的延长线上,点P在线段OB上时的重叠面积,利用三角形的面积计算公式求得答案即可;
(3)由于OC=$\sqrt{3}$,OA=3,OA⊥OC,则△OAC是含30°的直角三角形,分两种情况探讨:当△AMO以∠AMO为直角的直角三角形时;当△AMO以∠OAM为直角的直角三角形时;得出答案即可.
解答 解:(1)∵抛物线y=ax2+bx+$\sqrt{3}$经过A(-3,0),B(1,0)两点,
∴$\left\{\begin{array}{l}{9a-3b+\sqrt{3}=0}\\{a+b+\sqrt{3}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$;
则D点坐标为(-2,$\sqrt{3}$).
(2)∵点D与A横坐标相差1,纵坐标之差为$\sqrt{3}$,则tan∠DAP=$\sqrt{3}$,
∴∠DAP=60°,
又∵△APQ为等边三角形,
∴点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质可知:AP=AD=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2.
①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积.
AP=t,
∵∠QAP=60°,
∴点Q的纵坐标为t•sin60°=$\frac{\sqrt{3}}{2}$t,
∴S=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$t×t=$\frac{\sqrt{3}}{4}$t2.
②当2<t≤3时,如图: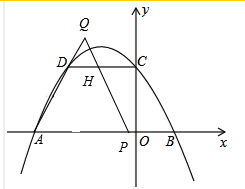
此时点Q在AD的延长线上,点P在OA上,
设QP与DC交于点H,
∵DC∥AP,
∴∠QDH=∠QAP=∠QHD=∠QPA=60°,
∴△QDH是等边三角形,
∴S=S△QAP-S△QDH,
∵QA=t,
∴S△QAP=$\frac{\sqrt{3}}{4}$t2.
∵QD=t-2,
∴S△QDH=$\frac{\sqrt{3}}{4}$(t-2)2,
∴S=$\frac{\sqrt{3}}{4}$t2-$\frac{\sqrt{3}}{4}$(t-2)2=$\sqrt{3}$t-$\sqrt{3}$.
③当3<t≤4时,如图: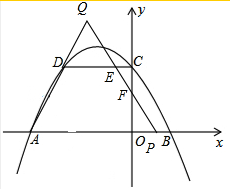
此时点Q在AD的延长线上,点P在线段OB上,
设QP与DC交于点E,与OC交于点F,过点Q作AP的垂涎,垂足为G,
∵OP=t-3,∠FPO=60°,
∴OF=OP•tan60°=$\sqrt{3}$(t-3),
∴S△FOP=$\frac{1}{2}$×$\sqrt{3}$(t-3)(t-3)=$\frac{\sqrt{3}}{2}$(t-3)2,
∵S=S△QAP-S△QDE-S△FOP,S△QAP-S△QDE=$\sqrt{3}$t-$\sqrt{3}$.
∴S=$\sqrt{3}$t-$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(t-3)2=-$\frac{\sqrt{3}}{2}$t2+4$\sqrt{3}$t-$\frac{11}{2}$$\sqrt{3}$.
综上所述,S与t之间的函数关系式为S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{4}{t}^{2}(0≤t≤2)}\\{\sqrt{3}t-\sqrt{3}(2<t≤3)}\\{-\frac{\sqrt{3}}{2}{t}^{2}+4\sqrt{3}t-\frac{11}{2}\sqrt{3}(3<t≤4)}\end{array}\right.$.
(3)∵OC=$\sqrt{3}$,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.
①当△AMO以∠AMO为直角的直角三角形时;如图: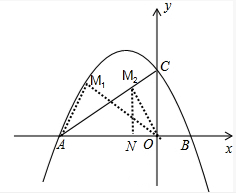
过点M2作AO的垂线,垂足为N,
∵∠M2AO=30°,AO=3,
∴M2O=$\frac{3}{2}$,
又∵∠OM2N=M2AO=30°,
∴ON=$\frac{1}{2}$OM2=$\frac{3}{4}$,M2N=$\sqrt{3}$ON=$\frac{3}{4}$$\sqrt{3}$,
∴M2的坐标为(-$\frac{3}{4}$,$\frac{3\sqrt{3}}{4}$).
同理可得M1的坐标为(-$\frac{9}{4}$,$\frac{3\sqrt{3}}{4}$).
②当△AMO以∠OAM为直角的直角三角形时;如图: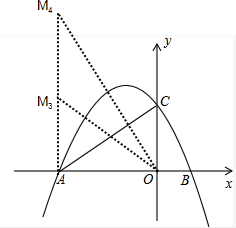
∵以M、O、A为顶点的三角形与△OAC相似,
∴$\frac{OA}{AM}$=$\sqrt{3}$,或$\frac{AM}{OA}$=$\sqrt{3}$,
∵OA=3,
∴AM=$\sqrt{3}$或AM=3$\sqrt{3}$,
∵AM⊥OA,且点M在第二象限,
∴点M的坐标为(-3,$\sqrt{3}$)或(-3,3$\sqrt{3}$).
综上所述,符合条件的点M的所有可能的坐标为(-3,$\sqrt{3}$),(-3,3$\sqrt{3}$),(-$\frac{9}{4}$,$\frac{3\sqrt{3}}{4}$),(-$\frac{3}{4}$,$\frac{3\sqrt{3}}{4}$).
点评 此题考查二次函数的综合运用,图形的运动,待定系数法求函数解析式,特殊角的三角函数,三角形的面积,分类讨论是解决问题的关键.


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
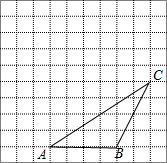 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
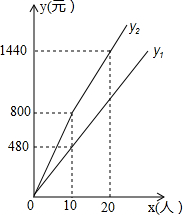 盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com