
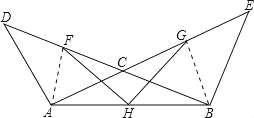
【题目】如图,已知AE、BD相交于点C,AC=AD,BC=BE,F、G、H分别是DC、CE、AB的中点.求证:
(1)HF=HG;
(2)∠FHG=∠DAC.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接AF,BG.根据等腰三角形的三线合一得到直角三角形,再根据直角三角形斜边上的中线等于斜边的一半进行证明;
(2)根据直角三角形斜边上的中线等于斜边的一半得到FH=BH,则∠HFB=∠FBH,同理∠AGH=∠GAH,则∠D=∠ACD=∠CAB+∠ABC=∠BFH+∠AGH.从而证明结论.
证明:(1)连接AF,BG,
∵AC=AD,BC=BE,F、G分别是DC、CE的中点,
∴AF⊥BD,BG⊥AE.
在直角三角形AFB中,
∵H是斜边AB中点,
∴FH=![]() AB.
AB.
同理得HG=![]() AB,
AB,
∴FH=HG.
(2)∵FH=BH,
∴∠HFB=∠FBH;
∵∠AHF是△BHF的外角,
∴∠AHF=∠HFB+∠FBH=2∠BFH;
同理∠AGH=∠GAH,∠BHG=∠AGH+∠GAH=2∠AGH,
∴∠ADB=∠ACD=∠CAB+∠ABC=∠BFH+∠AGH.
又∵∠DAC=180°﹣∠ADB﹣∠ACD,
=180°﹣2∠ADB,
=180°﹣2(∠BFH+∠AGH),
=180°﹣2∠BFH﹣2∠AGH,
=180°﹣∠AHF﹣∠BHG,
而根据平角的定义可得:∠FHG=180°﹣∠AHF﹣∠BHG,
∴∠FHG=∠DAC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
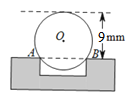
【题目】工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是_________毫米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点A(a+1,2),B(-a-5,2a+1).
(1)若线段AB∥y轴,求点A、B的坐标;
(2)当点B到y轴的距离是到x轴的距离4倍时,求点B所在的象限位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程![]() 中的分母化为整数,得
中的分母化为整数,得![]() =12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
=12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E从点A出发,以每秒
,点E从点A出发,以每秒![]() 个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转
个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转![]() 得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒
得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒![]()
![]() 用含t的代数式表示点E到边AB的距离;
用含t的代数式表示点E到边AB的距离;
![]() 当点G落在边AB上时,求t的值;
当点G落在边AB上时,求t的值;
![]() 连结BG,设
连结BG,设![]() 的面积为S个平方单位
的面积为S个平方单位![]() ,求S与t之间的函数关系式;
,求S与t之间的函数关系式;
![]() 直接写出正方形EFGH的顶点H,G分别与点A,C距离相等时的t值.
直接写出正方形EFGH的顶点H,G分别与点A,C距离相等时的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)解方程:![]()
(3)如图所示,小明将一张正方形纸片,剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条。如果两次剪下的长条面积正好相等,那么每个长条的面积为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com