
【题目】如图,四边形ABCD是平行四边形,CE⊥AD于点E,DF⊥BA交BA的延长线于点F.
(1)求证:△ADF∽△DCE;
(2)当AF=2,AD=6,且点E恰为AD中点时,求AB的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
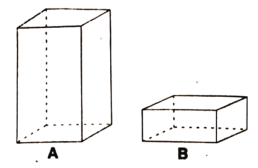
【题目】网购是现在人们常用的购物方式,通常网购的商品为防止损坏会采用盒子进行包装,![]() 均是容积为
均是容积为![]() 立方分米无盖的长方体盒子(如图).
立方分米无盖的长方体盒子(如图).
(1)图中![]() 盒子底面是正方形,
盒子底面是正方形,![]() 盒子底面是长方形,
盒子底面是长方形,![]() 盒子比
盒子比![]() 盒子高6分米,
盒子高6分米,![]() 和
和![]() 两个盒子都选用相同的材料制作成侧面和底面,制作底面的材料1.5元/平方分米,其中
两个盒子都选用相同的材料制作成侧面和底面,制作底面的材料1.5元/平方分米,其中![]() 盒子底面制作费用是
盒子底面制作费用是![]() 盒子底面制作费用的3倍,当
盒子底面制作费用的3倍,当![]() 立方分米时,求
立方分米时,求![]() 盒子的高(温馨提示:要求用列分式方程求解).
盒子的高(温馨提示:要求用列分式方程求解).
(2)在(1)的条件下,已知![]() 盒子侧面制作材料的费用是0.5元/平方分米,求制作一个
盒子侧面制作材料的费用是0.5元/平方分米,求制作一个![]() 盒子的制作费用是多少元?
盒子的制作费用是多少元?
(3)设![]() 的值为(2)中所求的一个
的值为(2)中所求的一个![]() 盒子的制作费用,请分解因式;
盒子的制作费用,请分解因式;![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,6),点B(4,3),P是x轴上的一个动点.作OQ⊥AP,垂足为点Q,连接QB,则△AQB的面积的最大值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
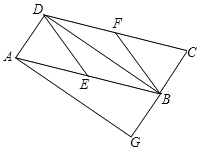
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数( )
①近似数![]() 精确到十分位:
精确到十分位:
②在![]() ,
,![]() ,
,![]() ,
,![]() 中,最小的数是
中,最小的数是![]()
③如图①所示,在数轴上点![]() 所表示的数为
所表示的数为![]()
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在![]() 内一点
内一点![]() 到这三条边的距离相等,则点
到这三条边的距离相等,则点![]() 是三个角平分线的交点
是三个角平分线的交点
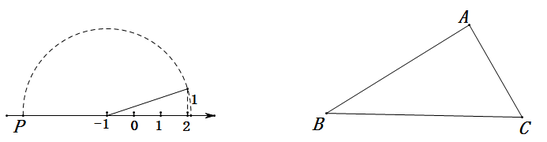
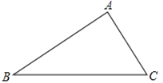
图① 图②
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
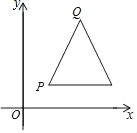
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若PQ为某个等腰三角形的腰,且该等腰三角形的底边与x轴平行,则称该等腰三角形为点P,Q的“相关等腰三角形”.下图为点P,Q的“相关等腰三角形”的示意图.
(1)已知点A的坐标为(0,1),点B的坐标为(-![]() ,0),则点A,B的“相关等腰三角形”的顶角为 °;
,0),则点A,B的“相关等腰三角形”的顶角为 °;
(2)若点C的坐标为(0,![]() ),点D在直线y=4
),点D在直线y=4![]() 上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
(3)⊙O的半径为![]() ,点N在双曲线y=﹣
,点N在双曲线y=﹣![]() 上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:
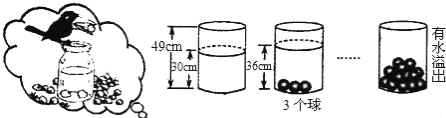
(1)放入一个小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的函数关系式;
(3)当量桶中水面上升至距离量桶顶部3cm时,应在量桶中放入几个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,有一等腰直角三角形OAB,∠OAB=90°,直角边OA在x轴正半轴上,且OA=1,将Rt△OAB绕原点顺时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OA1B1(即A1O=2AO).同理,将Rt△OA1B1顺时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OA2B2……依此规律,得到等腰直角三角形OA2014B2014,则A2014点的坐标为( )
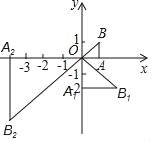
A. (0,22014) B. (0,﹣22014) C. (22014,0) D. (﹣22014,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com