
【题目】如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( ) 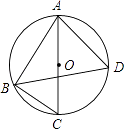
A.45°
B.85°
C.90°
D.95°
【答案】B
【解析】解:∵AC是⊙O的直径, ∴∠ABC=90°,
∵∠C=50°,
∴∠BAC=40°,
∵∠ABC的平分线BD交⊙O于点D,
∴∠ABD=∠DBC=45°,
∴∠CAD=∠DBC=45°,
∴∠BAD=∠BAC+∠CAD=40°+45°=85°,
故选:B.
【考点精析】掌握圆心角、弧、弦的关系和圆周角定理是解答本题的根本,需要知道在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 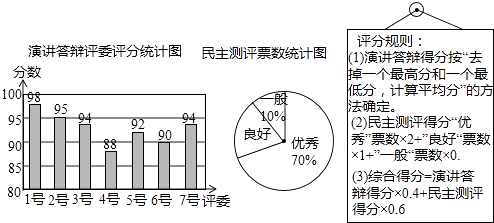
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上所对应的点分别是A,B.C三点,且a,b满足,①多项式![]() x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
(1)请在图1的数轴上描出A,B,C三点,并直接写出a,b,c三数之间的大小关系 用“<”连接);
(2)点P为数轴上C点右侧一点,且点P到A点的距离是到C点距高的2倍,求点P在数轴上所对应的有理数;
(3)点A在数轴上以每秒1个单位长度的速度向左运动,同时点B和点C在数轴上分别以每秒m个单位长度和4个单位长度的速度向右运动(其中m<4),若在整个运动的过程中,点B到点A的距离与点B到点C的距离差始终不变,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: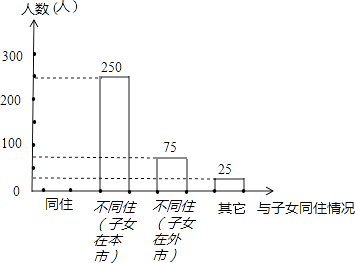
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=k(x+1)(x﹣ ![]() )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠B=60°,边AB=BC=8cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是每秒1cm,点Q运动的速度是每秒2cm,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
解答下列问题:
(1)AP= ,BP= ,BQ= .(用含t的代数式表示,t≤4)
(2)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(3)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com