
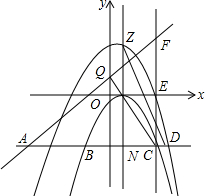
 Èçͼ£¬̉ÑÖª¹ưµă£¨0£¬-$\frac{1}{4}$£©µÄÅ×ÎïÏßC1£ºy=ax2+bx+cµÄ¶¥µăΪQ£¨1£¬0£©£¬ÏÖ½«¸ĂÅ×ÎïÏßÉÏËùÓеăµÄ×Ư×ø±ê¼Óh£¨h£¾0£©£¬ºá×ø±ê²»±ä£¬µĂµ½ĐµÄÅ×ÎïÏߣ¬¼ÇΪC2£¬ÔÚyÖáµÄ¸º°ëÖá×÷̉»̀ơƽĐĐÓÚxÖáµÄÖ±Ïߣ¬ÓëÁ½̀ơÅ×ÎïÏß½»ÓÚA¡¢B¡¢C¡¢DËÄµă£¬Ö±ÏßADÓëxÖáµÄ¾àÀëÊÇm2£¨m£¾0£©
Èçͼ£¬̉ÑÖª¹ưµă£¨0£¬-$\frac{1}{4}$£©µÄÅ×ÎïÏßC1£ºy=ax2+bx+cµÄ¶¥µăΪQ£¨1£¬0£©£¬ÏÖ½«¸ĂÅ×ÎïÏßÉÏËùÓеăµÄ×Ư×ø±ê¼Óh£¨h£¾0£©£¬ºá×ø±ê²»±ä£¬µĂµ½ĐµÄÅ×ÎïÏߣ¬¼ÇΪC2£¬ÔÚyÖáµÄ¸º°ëÖá×÷̉»̀ơƽĐĐÓÚxÖáµÄÖ±Ïߣ¬ÓëÁ½̀ơÅ×ÎïÏß½»ÓÚA¡¢B¡¢C¡¢DËÄµă£¬Ö±ÏßADÓëxÖáµÄ¾àÀëÊÇm2£¨m£¾0£©·ÖÎö £¨1£©ÀûÓĂµă£¨0£¬-$\frac{1}{4}$£©ºÍÅ×ÎïÏßC1£ºy=ax2+bx+cµÄ¶¥µăΪQ£¨1£¬0£©£¬´úÈ뺯Êư½âÎöʽ£¬¼´¿É½â´đ£»
£¨2£©ÏÈÈ·¶¨Å×ÎïÏßC2µÄ½âÎöʽΪy=-$\frac{1}{4}$£¨x-1£©2+4£¬ÔÙÇó³öµăEµÄ×ø±êΪ£¨5£¬0£©£¬µăFµÄ×ø±êΪ£¨5£¬6£©£¬¼´FE=6£®ÉèÔÚ¡÷EFPÖĐ£¬±ßEFÉϵĸßΪd£®·ÖÁ½ÖÖÇé¿ö½øĐĐ̀ÖÂÛ£º¢Ùµ±µăPÔÚEFµÄ×ó²àʱ£¬d=5-xP¢Úµ±µăPÔÚEFµÄÓ̉²àʱ£¬d=xP-5£¬¸ù¾ƯS¡÷EFP¡Ü6£¬ÁĐ³ö²»µÈʽ£¬¼´¿É½â´đ£»
£¨3£©ÏÈÇó³öµăCµÄ×ø±êΪ£¨1+2m£¬-m2£©£®µăAµÄ×ø±êΪ£¨-1-2m£¬-m2£©£¬´Ó¶øÈ·¶¨DM=AM=1-£¨-1-2m£©=2+2m£®ÔÙÉèÅ×ÎïÏßC2µÄ½âÎöʽΪy=-$\frac{1}{4}$£¨x-1£©2+h£®½«µăAµÄ×ø±ê´úÈëÅ×ÎïÏßC2µÄ½âÎöʽÖĐ£¬Çó³öh=2m+1£¬´Ó¶øµĂµ½MN=h+m2=2m+1+m2£¬¸ù¾Ưtan¡ÏMDN=$\frac{MN}{DM}$=$\frac{2m+1+{m}^{2}}{2+2m}$£¬tan¡ÏMCQ=$\frac{QM}{CM}$=$\frac{{m}^{2}}{2m}$£¬¼´¿É½â´đ£®
½â´đ ½â£º£¨1£©¡ßÅ×ÎïÏßC1£ºy=ax2+bx+c¹ưµă£¨0£¬-$\frac{1}{4}$£©£¬
¡àc=-$\frac{1}{4}$£®
ÓÖ¡ßÆ䶥µăΪQ£¨1£¬0£©£¬
¡àa+b+c=0£¬-$\frac{b}{2a}$=1£¬
¡à½âµĂ£ºa=-$\frac{1}{4}$£¬b=$\frac{1}{2}$£¬
¡àÅ×ÎïÏßC1µÄ½âÎöʽΪy=-$\frac{1}{4}$x2+$\frac{1}{2}$x-$\frac{1}{4}$£»
£¨2£©¡ßÅ×ÎïÏßC1µÄ½âÎöʽΪy=-$\frac{1}{4}$x2+$\frac{1}{2}$x-$\frac{1}{4}$£¬
ƠûÀí¿ÉµĂy=-$\frac{1}{4}$£¨x-1£©2£®
¡ß½«Å×ÎïÏßC1ÉÏËùÓеăµÄ×Ư×ø±ê¶¼¼Óh¡¢ºá×ø±ê²»±ä¿ÉµĂµ½Å×ÎïÏßC2£¬h=4£¬
¡àÅ×ÎïÏßC2µÄ½âÎöʽΪy=-$\frac{1}{4}$£¨x-1£©2+4£¬
¡àµăEµÄ×ø±êΪ£¨5£¬0£©£®
̉×ÖªEF¡ÍxÖᣬ
¡àµăFµÄºá×ø±êΪ5£®
¡ßµăFÔÚÖ±Ïßy=x+1ÉÏ£¬
¡àµăFµÄ×ø±êΪ£¨5£¬6£©£¬¼´FE=6£®
ÉèÔÚ¡÷EFPÖĐ£¬±ßEFÉϵĸßΪd£®
¢Ùµ±µăPÔÚEFµÄ×ó²àʱ£¬d=5-xP£¬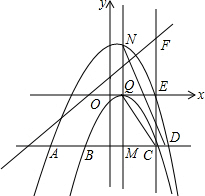
¡àS¡÷EFP=$\frac{1}{2}$EF•d=$\frac{1}{2}$¡Á6¡Á£¨5-xP£©¡Ü6£¬
¡àxP¡Ư3£®
¢Úµ±µăPÔÚEFµÄÓ̉²àʱ£¬d=xP-5£¬
¡àS¡÷EFP=$\frac{1}{2}$EF•d=$\frac{1}{2}$¡Á6¡Á£¨xP-5£©¡Ü6£¬
¡àxP¡Ü7£¬
¡àµăPºá×ø±êxPµÄÈ¡Öµ·¶Î§ÊÇ3¡ÜxP¡Ü7£®
£¨3£©¡ßÖ±ÏßADÓëxÖáµÄ¾àÀëÊÇm2£¬
¡àµăB£¬CµÄ×Ư×ø±êΪ-m2£¬
¡à-$\frac{1}{4}$£¨x-1£©2=-m2£¬
½âµĂx1=1+2m£¬x2=1-2m£¬
¡àµăCµÄ×ø±êΪ£¨1+2m£¬-m2£©£®
¡ßMNÊÇÅ×ÎïÏßC1µÄ¶Ô³ÆÖᣬ
¡àCM=1+2m-1=2m£®
¡ßµăA£¬C¹ØÓÚyÖá¶Ô³Æ£¬
¡àµăAµÄ×ø±êΪ£¨-1-2m£¬-m2£©£¬
¡àDM=AM=1-£¨-1-2m£©=2+2m£®
ÉèÅ×ÎïÏßC2µÄ½âÎöʽΪy=-$\frac{1}{4}$£¨x-1£©2+h£®
½«µăAµÄ×ø±ê´úÈëÅ×ÎïÏßC2µÄ½âÎöʽÖĐ£¬
¡à-$\frac{1}{4}$£¨-1-2m-1£©2+h=-m2£¬
¡àh=2m+1£¬
¡àMN=h+m2=2m+1+m2£¬
¡àtan¡ÏMDN=$\frac{MN}{DM}$=$\frac{2m+1+{m}^{2}}{2+2m}$£¬
tan¡ÏMCQ=$\frac{QM}{CM}$=$\frac{{m}^{2}}{2m}$£¬
¡à$\frac{tan¡ÏMDN}{tan¡ÏMCQ}$=$\frac{m+1}{m}$£®
µăÆÀ ±¾̀⿼²éÁ˶₫´Îº¯ÊưµÄĐÔÖÊ£¬Çó¶₫´Îº¯Êư½âÎöʽ¡¢Èư½Çº¯Êư£¬½â¾ö±¾̀⣨2£©µÄ¹Ø¼üÊǽøĐĐ·ÖÀà̀ÖÂÛ£¬½â¾ö±¾̀⣨3£©µÄ¹Ø¼üÊǺ¯Êư½âÎöʽ¶¥µăʽµÄÓ¦ÓĂ£®


 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 2 | B£® | $\sqrt{2}$ | C£® | $¡À\sqrt{2}$ | D£® | $\frac{1}{2}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
 Èçͼ£¬¡÷ABCÖĐ£¬¡ÏABC=40¡ă£¬BDƽ·Ö¡ÏABC£¬BC=BD+AD£®ÇóÖ¤£ºAB=AC£®
Èçͼ£¬¡÷ABCÖĐ£¬¡ÏABC=40¡ă£¬BDƽ·Ö¡ÏABC£¬BC=BD+AD£®ÇóÖ¤£ºAB=AC£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 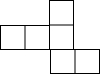 | B£® | 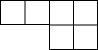 | C£® | 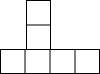 | D£® | 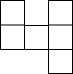 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com