练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

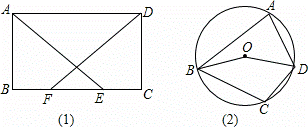
    （1）如图，在矩形ABCD中，BF=CE，求证：AE=DF；

    （2）如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，求∠BCD的度数．

     


    （1）证明：∵四边形ABCD是矩形，

    ∴AB=CD，∠B=∠C=90°，

    ∵BF=CE，

    ∴BE=CF，

    在△ABE和△DCF中

     

    ∴△ABE≌△DCF，

    ∴AE=DF；

    （2）解：∵∠BOD=160°，

    ∴∠BAD= ∠BOD=80°，

    ∵A、B、C、D四点共圆，

    ∴∠BCD+∠BAD=180°，

    ∴∠BCD=100°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    不等式组的解集在数轴上可表示为（　　）

    A．      B．      C．      D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在10×10的正方形网格中，点A，B，C，D均在格点上，以点A为位似中心画四边形AB′C′D′，使它与四边形ABCD位似，且相似比为2．

    （1）在图中画出四边形AB′C′D′；

    （2）填空：△AC′D′是　　　　　　三角形．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形，做成一个无盖的盒子，已知盒子的容积为300cm3，则原铁皮的边长为（　　）

    　    A． 10cm      B． 13cm      C． 14cm      D． 16cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小球在如图所示的地板上自由滚动，并随机地停留在某块方砖上，每一块方砖的除颜色外完全相同，它最终停留在黑色方砖上的概率是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y=ax2+bx+4（a≠0）过点A（1，﹣1），B（5，﹣1），与y轴交于点C．

    （1）求抛物线的函数表达式；

    （2）如图1，连接CB，以CB为边作▱CBPQ，若点P在直线BC上方的抛物线上，Q为坐标平面内的一点，且▱CBPQ的面积为30，求点P的坐标；

    （3）如图2，⊙O1过点A、B、C三点，AE为直径，点M为 上的一动点（不与点A，E重合），∠MBN为直角，边BN与ME的延长线交于N，求线段BN长度的最大值．

     

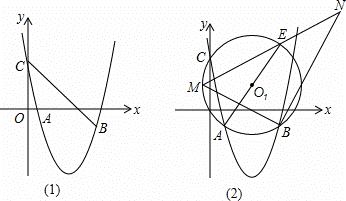
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    以下图形中对称轴的数量小于3的是(    )

                       

    A．           B．         C．            D．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


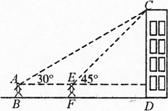
    小敏同学想测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°(BFD在同一直线上)．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据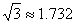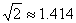：，．结果保留整数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将抛物线y=﹣x2+2x+3在x轴上方的部分沿x轴翻折至x轴下方，图象的剩余部分不变，得到一个新的函数图象，那么直线y=x+b与此新图象的交点个数的情况有（　　）种．

    　   A．6                     B． 5                           C．                             4    D．   3

    查看答案和解析>>

    同步练习册答案