
【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求![]() 的值;
的值;
(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.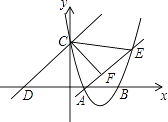
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
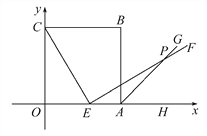
【题目】如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ![]() ;
;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 . 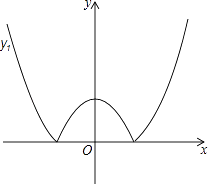
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地与丙地由公路连接,乙地在甲、丙两地之间,一辆汽车在下午1点钟从离甲地10千米的M地出发向乙地匀速前进,15分钟后离甲地20千米,当汽车行驶到离甲地150千米的乙地时,接到通知要在下午5点前赶到离乙地30千米的丙地.汽车若按原速能否按时到达?若能,是在几点几时到达;若不能,车速应提高到多少才能按时到达?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求值问题中,我们经常遇到利用整体思想来解决问题.
例如1:已知:x+2y﹣3z=2,2x+y+6z=1,求:x+y+z的值
解:令x+2y﹣3z=2﹣﹣﹣﹣﹣①2x+y+6z=1﹣﹣﹣﹣﹣﹣②
①+②得3x+3y+3z=3所以x+y+z=1
已知![]() 求x+2y的值
求x+2y的值
解:①×2得:2x+2y=﹣10③
②﹣③得:x+2y=11
利用材料中提供的方法,解决下列问题
(1)已知:关于x,y的二元一次方程组![]() 的解满足x﹣y=6,求m的值
的解满足x﹣y=6,求m的值
(2)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙咱盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com