
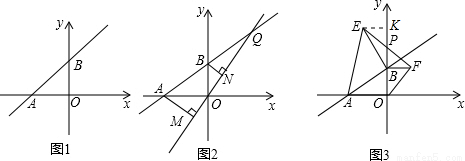
(本题12分)如图①所示,直线L: 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点。
轴正半轴分别交于A、B两点。
(1)当OA=OB时,试确定直线L的解析式;



(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,试说明MN=AM+BN。
(3)当 取不同的值时,点B在
取不同的值时,点B在 轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交
轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交 轴于P点,如图③。
轴于P点,如图③。
问:当点B在 y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由。
(1)y=x+5 (2)7 (3)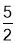
【解析】
试题分析:(1)由直线L解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
(2)由OA=OB,对顶角相等,且一对直角相等,利用AAS得到△AMO≌△ONB,用对应线段相等求长度;
(3)如图,作EK⊥y轴于K点,利用AAS得到△AOB≌△BKE,利用全等三角形对应边相等得到OA=BK,EK=OB,再利用AAS得到△PBF≌△PKE,寻找相等线段,并进行转化,求PB的长.
试题解析: 【解析】
(1)∵直线L:y=mx+5m,
∴A(-5,0),B(0,5m),
由OA=OB,
得5m=5,m=1,
∴直线解析式为:y=x+5;
(2)在△AMO和△OBN中,
 ,
,
∴△AMO≌△ONB(AAS),
∴AM=ON=4,
∴BN=OM=3,
则MN=OM+ON=4+3=7;
(3)如图,作EK⊥y轴于K点,
∵△ABE为等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠EBK+∠ABO=90°,
∵∠EBK+∠BEK=90°,
∴∠ABO=∠BEK,
在△AOB和△BKE中,
 ,
,
∴△AOB≌△BKE(AAS),
∴OA=BK,EK=OB,
∵△OBF为等腰直角三角形,
∴OB=BF,
∴EK=BF,
在△EKP和△FBP中,
 ,
,
∴△PBF≌△PKE(AAS),
∴PK=PB,
∴PB=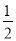 BK=
BK=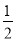 OA=
OA=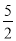 .
.
考点:一次函数的解析式,一次函数的图像与性质,等腰直角三角形的性质,全等三角形的判定与性质


科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:解答题
网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:选择题
如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
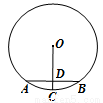
A.1cm B.2cm C.2.5cm D.5cm
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第四次月考数学试卷(解析版) 题型:填空题
若函数 的部分图象如图所示,由图可知,关于x的方程
的部分图象如图所示,由图可知,关于x的方程 的
的
一根是3,则另一根为________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第四次月考数学试卷(解析版) 题型:选择题
已知实数x满足(x2-x) 2-4(x2-x)-12=0,则x2-x=________ ( )
A.-2 B.6或-2 C.6 D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都十校八年级12月联谊月考数学试卷(解析版) 题型:解答题
(本题8分) 求一个正数的算术平方根,有些数可以直接求得,如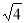 ,有些数则不能直接求得,如
,有些数则不能直接求得,如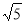 ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知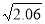
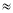 1.435,求下列各数的算术平方根:
1.435,求下列各数的算术平方根:
①0.0206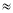 ; ②20600
; ②20600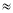 ;
;
(3)根据上述探究过程类比研究一个数的立方根已知
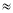 1.260,则
1.260,则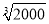
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都十校八年级12月联谊月考数学试卷(解析版) 题型:填空题
如图,已知一次函数 和
和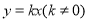 的图象交于点
的图象交于点 ,则一元一次不等式
,则一元一次不等式 的解集是 。
的解集是 。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市七年级上学期期中数学试卷(解析版) 题型:解答题
(本题满分6分)
(1)如图1,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△AEG的面积。

(2)如图2,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△DBF的面积。

(3)如图,正方形ABCD、正方形CEFG和正方形MNHF的位置如图所示,点G在线段AN上,已知正方形CEFG的边长为6,则△AEN的面积为 (请直接写出结果,不需要过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com