
【题目】函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).
(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;
(2)若过原点的两条直线OA、OB分别与二次函数y=![]() x2交于点A(m,
x2交于点A(m,![]() m2)和点B(n,
m2)和点B(n,![]() n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.
【答案】(1)定点(﹣2,0);定点(1,2019)、(0,2019);(2)定点为E(2,4);![]()
【解析】
(1)y=kx+2k=k(x+2),当x=﹣2时,y=0,故过定点(﹣2,0),即可求解;
(2)直线AB的表达式为: ![]() ,则tan∠AOM=tan∠OBM,即:
,则tan∠AOM=tan∠OBM,即: 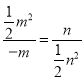 ,解得
,解得![]() ,故直线AB的表达式为:
,故直线AB的表达式为: ![]() ,当x=0时,y=﹣2,故直线AB过点(0,﹣2);
,当x=0时,y=﹣2,故直线AB过点(0,﹣2);
(3)直线CD的表达为:y=(m+n)x﹣mn,则m+n=k,mn=﹣2k﹣5,tan∠CEM=tan∠EDN,即:t2+(m+n)t+mn=﹣1,即:t2﹣4+(t﹣2)k=0,即可求解.
解:(1)y=kx+2k=k(x+2),当x=﹣2时,y=0,故过定点(﹣2,0);
y=kx2﹣kx+2019=![]() ,当x=0或1时,y=2019,故过定点(1,2019)、(0,2019);
,当x=0或1时,y=2019,故过定点(1,2019)、(0,2019);
(2)将点A、B的坐标代入一次函数表达式:y=kx+b并解得:
直线AB的表达式为: ![]()
分别过点A、B作x轴的垂线于点M、N,则∠AOM=∠OBN,
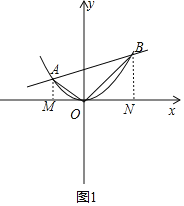
则tan∠AOM=tan∠OBN,即: 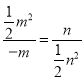 ,解得:
,解得: ![]()
故直线AB的表达式为: ![]() ,当x=0时,y=2,
,当x=0时,y=2,
故直线AB过点(0,2);
(3)设点C、D的坐标分别为:(m,m2)、(n,n2),
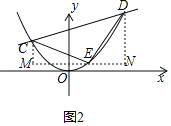
同理可得:直线CD的表达为:![]()
则m+n=k,mn=﹣2k﹣5,
设点E(t,t2),
同理可得:tan∠CEM=tan∠EDN,即:![]()
化简得:t2+(m+n)t+mn=﹣1,
即:t2﹣4+(t﹣2)k=0,
当t=2时,上式横成立,
故定点为E(2,4);
直线CD:y=kx+2k+5过定点H(﹣2,5),
∵点到直线的距离≤EH,
故点E到直线的最大距离为![]()


科目:初中数学 来源: 题型:
【题目】“红灯停,绿灯行”是我们过路口遇见交通信号灯时必须遵守的规则.小明每天从家骑自行车上学要经过三个路口,假如每个路口交通信号灯中红灯和绿灯亮的时间相同,且每个路口的交通信号灯只安装了红灯和绿灯.那么某天小明从家骑车去学校上学,经过三个路口抬头看到交通信号灯.
(1)请画树状图,列举小明看到交通信号灯可能出现的所有情况;
(2)求小明途经三个路口都遇到红灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
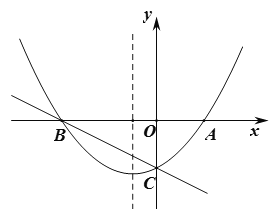
【题目】如图,对称轴是![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 若点
若点![]() 是直线
是直线![]() 下方的抛物线上的动点,求
下方的抛物线上的动点,求![]() 的面积的最大值;
的面积的最大值;
![]() 若点
若点![]() 在抛物线对称轴左侧的抛物线上运动,过点
在抛物线对称轴左侧的抛物线上运动,过点![]() 作
作![]() 铀于点
铀于点![]() ,交直线
,交直线![]() 于点
于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在对称轴上是否存在一点
在对称轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,请求出
的周长最小,若存在,请求出![]() 点的坐标和
点的坐标和![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新的教学改革的推动下,某中学初年级积极推进英语小班教学.为了了解一段时间以来的英语小班教学的学习效果,年级组织了多次定时测试,现随机选取甲,乙两个班,从中各抽取20名同学在某一次定时测试中的英语成绩,过程如下,请补充完整
收集数据:
甲班的20名同学的英语成绩统计(单位:分)
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计(满分为100分)(单位:分)
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
数量分数/ 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据:
请回答下列问题:
(1)完成下表:
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a= |
乙班 | 80.35 | b= | 78 |
甲班成绩得分扇形图(x表示分数)
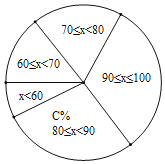
(2)在班成绩行分的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数 ,c= .
(3)根据以上数据,你认为 班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是: ;
(4)若英语定时成绩不低于80分为优秀,请估计全年级1600人中优秀人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
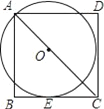
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的
⊙ O与BC相切于点E.
(1)求证:CD是⊙ O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com