
【题目】在新的教学改革的推动下,某中学初年级积极推进英语小班教学.为了了解一段时间以来的英语小班教学的学习效果,年级组织了多次定时测试,现随机选取甲,乙两个班,从中各抽取20名同学在某一次定时测试中的英语成绩,过程如下,请补充完整
收集数据:
甲班的20名同学的英语成绩统计(单位:分)
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计(满分为100分)(单位:分)
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
数量分数/ 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据:
请回答下列问题:
(1)完成下表:
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a= |
乙班 | 80.35 | b= | 78 |
甲班成绩得分扇形图(x表示分数)
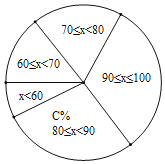
(2)在班成绩行分的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数 ,c= .
(3)根据以上数据,你认为 班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是: ;
(4)若英语定时成绩不低于80分为优秀,请估计全年级1600人中优秀人数为多少?
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】为看丰富学生课余文化生活,某中学组织学生进行才艺比赛,每人只能从以下五个项目中选报一项:![]() .书法比赛,
.书法比赛,![]() .绘画比赛,
.绘画比赛,![]() .乐器比赛,
.乐器比赛,![]() .象棋比赛,
.象棋比赛,![]() .围棋比赛根据学生报名的统计结果,绘制了如下尚不完整的统计图:
.围棋比赛根据学生报名的统计结果,绘制了如下尚不完整的统计图:
图1 各项报名人数扇形统计图:
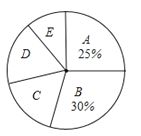
图2 各项报名人数条形统计图:

根据以上信息解答下列问题:
(1)学生报名总人数为 人;
(2)如图1项目D所在扇形的圆心角等于 ;
(3)请将图2的条形统计图补充完整;
(4)学校准备从书法比赛一等奖获得者甲、乙、丙、丁四名同学中任意选取两名同学去参加全市的书法比赛,求恰好选中甲、乙两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
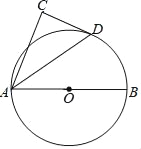
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).
(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;
(2)若过原点的两条直线OA、OB分别与二次函数y=![]() x2交于点A(m,
x2交于点A(m,![]() m2)和点B(n,
m2)和点B(n,![]() n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
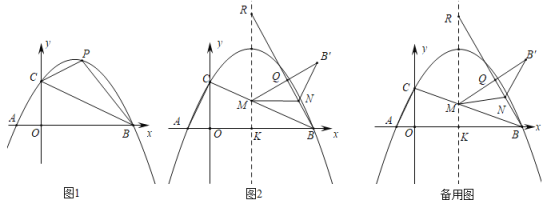
(1)点P为线段BC上方抛物线上(不与B、C重合)的一动点,连接PC、PB,当△PBC面积最大时,在y轴找点D,使得PD﹣![]() OD的值最小时,求这个最小值.
OD的值最小时,求这个最小值.
(2)如图2,抛物线对称轴与x轴交于点K,与线段BC交于点M,在对称轴上取一点R,使得KR=12(点R在第一象限),连接BR.已知点N为线段BR上一动点,连接MN,将△BMN沿MN翻折到△B'MN.当△B'MN与△BMR重叠部分(如图中的△MNQ)为直角三角形时,直接写出此时点B'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为![]() 、
、![]() 、
、![]() ,若AD=2,AB=
,若AD=2,AB=![]() ,∠A=60°,则
,∠A=60°,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
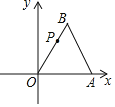
【题目】如图,以边长为4![]() +4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
+4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com