【题目】先化简，再求值：
（1）
其中
．
（2）
其中
．
【答案】（1）2x4y；12（2）9a4＋14a3b3b2；7
【解析】
（1）利用多项式的运算规则和完全平方式的展开式对整式进行化简，然后再把x＝2，y＝2，代入求值；
（2）同样根据多项式的运算规则和完全平方式的展开式，从左到右进行化简约分，然后再把a＝1，b＝2，代入求值．
（1）
＝（4x2＋4xy＋y2y24xy8xy）×
＝（4x28xy）×
＝2x4y
把x＝2，y＝2代入上式，
原式＝2x4y＝2×24×（2）＝12；
（2）
＝9a4＋18a3b（9ab3＋12a4b2）×
＝9a4＋18a3b3b24a3b
＝9a4＋14a3b3b2
把a＝1，b＝2，代入上式，
原式＝9a4＋14a3b3b2＝914×（2）3×4＝7．
53天天练系列答案科目：初中数学 来源： 题型：
【题目】已知在纸面上有一数轴（如图），折叠纸面．
（1）若1表示的点与
表示的点重合，则
表示的点与数 表示的点重合；
（2）若表示的点与3表示的点重合，回答以下问题：
①5表示的点与数 表示的点重合；
②若数轴上
、
两点之间的距离为9（在的左侧），且、两点经折叠后重合，求、两点表示的数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数学兴趣小组想测量电线杆AB的高度，他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD＝4 m，BC＝10 m，CD与地面成30°角，且此时测得高1 m的标杆的影长为2 m，则电线杆的高度为________m(结果保留根号)．
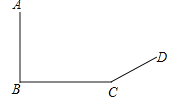
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB＝20cm，点P从点A出发，沿AB以2cm/s的速度匀速向终点B运动；同时点Q从点B出发，沿BA以4cm/s的速度匀速向终点A运动，设运动时间为ts
（1）填空：PA＝ cm；BQ＝ cm；（用含t的代数式表示）
（2）当P、Q两点相遇时，求t的值；
（3）探究：当PQ两点相距5cm时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在Rt△ABC中,∠C=90°,O是AB上一点, ⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是__.
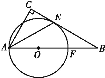
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】你会对多项式(x2+5x+2)(x2+5x+3)﹣12分解因式吗？对结构较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，能使复杂的问题简单化、明朗化．从换元的个数看，有一元代换、二元代换等．
对于(x2+5x+2)(x2+5x+3)﹣12．
解法一：设x2+5x＝y，
则原式＝(y+2)(y+3)﹣12＝y2+5y﹣6＝(y+6)(y﹣1)
＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．
解法二：设x2+5x+2＝y，
则原式＝y(y+1)﹣12＝y2+y﹣12＝(y+4)(y﹣3)
＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．
解法三：设x2+2＝m，5x＝n，
则原式＝(m+n)(m+n+1)﹣12＝(m+n)2+(m+n)﹣12＝(m+n+4)(m+n﹣3)
＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．
按照上面介绍的方法对下列多项式分解因式：
(1)(x2+x﹣4)(x2+x+3)+10；
(2)(x+1)(x+2)(x+3)(x+6)+x2；
(3)(x+y﹣2xy)(x+y﹣2)+(xy﹣1)2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,PA,PB,DE切⊙O于点A,B,C,D在PA上,E在PB上,
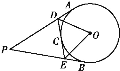
(1)若PA=10,求△PDE的周长;
(2)若∠P=50°,求∠O的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点C在线段AB上，AC = 8 cm，CB = 6 cm，点M、N分别是AC、BC的中点.
（1）求线段MN的长.
（2）若C为线段AB上任意一点，满足AC+CB=a(cm)，其他条件不变，你能猜想出MN的长度吗？并说明理由.
（3）若C在线段AB的延长线上，且满足AC-CB=b(cm)，M、N分别为AC、BC的中点，你能猜想出MN的长度吗？请画出图形，写出你的结论，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
