
【题目】你会对多项式(x2+5x+2)(x2+5x+3)﹣12分解因式吗?对结构较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),能使复杂的问题简单化、明朗化.从换元的个数看,有一元代换、二元代换等.
对于(x2+5x+2)(x2+5x+3)﹣12.
解法一:设x2+5x=y,
则原式=(y+2)(y+3)﹣12=y2+5y﹣6=(y+6)(y﹣1)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
解法二:设x2+5x+2=y,
则原式=y(y+1)﹣12=y2+y﹣12=(y+4)(y﹣3)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
解法三:设x2+2=m,5x=n,
则原式=(m+n)(m+n+1)﹣12=(m+n)2+(m+n)﹣12=(m+n+4)(m+n﹣3)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
按照上面介绍的方法对下列多项式分解因式:
(1)(x2+x﹣4)(x2+x+3)+10;
(2)(x+1)(x+2)(x+3)(x+6)+x2;
(3)(x+y﹣2xy)(x+y﹣2)+(xy﹣1)2.
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F,∠EDF=38°,则∠DBE的度数是( )
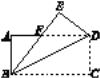
A. 25° B. 26° C. 27° D. 38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为_____.
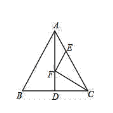
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ⊙O的半径是1,直线AB与x轴交于点P(x,0),且与x轴的正半轴夹角为45°,若直线AB与⊙O有公共点,则x值的范围是( )
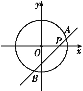
A. -1≤x≤1 B. -![]() ≤x≤
≤x≤![]() C. -
C. -![]() <x<
<x<![]() D. 0≤x≤
D. 0≤x≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行单项式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根据你发现的规律,解答下列问题:
(1)第①行的第8个单项式为 ;
(2)第②行的第9个单项式为 ;
(3)第③行的第n个单项式为 (用含n的式子表示);
(4)取每行的第8个单项式,令这三个单项式的和为A.
当![]() 时,求A的值.
时,求A的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点.
(1)如图2,数轴上点A、B表示的数分别为-4、12,点D是线段AB的三等分点,求点D在数轴上所表示的数;
(2)在(1)的条件下,点P从点A出发以每秒1个单位长度的速度在数轴上向右运动;点Q从点B出发,在数轴上先向左运动,与点P重合后立刻改变方向与点P同向而行,且速度始终为每秒3个单位长度,点P、Q同时出发,设运动时间为t秒.
①用含t的式子表示线段AQ的长度;
②当点P是线段AQ的三等分点时,求点P在数轴上所表示的数.
![]()
图1

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形” .下列判断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为![]() D. 事件M发生的概率为
D. 事件M发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com