
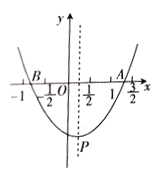
【题目】如图,抛物线![]() (a,b,c是常数,且
(a,b,c是常数,且![]() )与x轴交于A、B两点,顶点P(m,n),下列结论中,其中正确的有( )
)与x轴交于A、B两点,顶点P(m,n),下列结论中,其中正确的有( )
①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于x的方程
;③关于x的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,△ABP为等腰直角三角形
时,△ABP为等腰直角三角形
A.①②B.③④C.②④D.②③
【答案】C
【解析】
利用二次函数的性质一一判断即可。
∵![]() ,a>0 ∴a>-b,
,a>0 ∴a>-b,
∵x=-1时,y>0, ∴a-b+c>0,
∴2a+c>a-b+c>0,故①错误,
若(![]() ,y1),(-
,y1),(-![]() ,y2)(
,y2)(![]() ,y3)在抛物线上,
,y3)在抛物线上,

由图象法可知,y1>y2>y3;故②正确,
∵抛物线与直线y=t有交点时,方程ax2+bx+c=t有解,t≥n,
∴ax2+bx+c-t=0有实数解
要使得ax2+bx+k=0有实数解,则k=c-t≤c-n;故③错误,
设抛物线的对称轴交x轴于H
∵![]()
∴b2-4ac=4
∴x=![]()
∴|x1-x2|=![]()
∴AB=2PH,
∵BH=AH
∴PH=BH=AH
∴△PAB是直角三角形,
∵PA=PB,
∴△PAB是等腰直角三角形;故④正确
故选C


科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
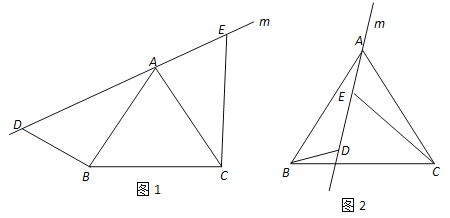
【题目】探索与证明:(1)如图1,直线m经过正三角形ABC的顶点A,在直线m上取两点 D,E,使得∠ADB=60°,∠AEC=60°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明;
(2)将(1)中的直线m绕点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.通过观察或测量,请直接写出线段BD,CE与DE之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
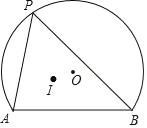
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
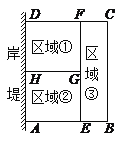
(1)求AE的长(用x的代数式表示)
(2)当y=108m2时,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
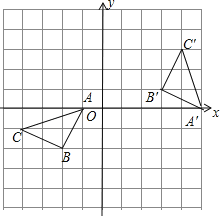
【题目】如图所示,在正方形网格中,△ABC的顶点坐标分别为(﹣1,0),(﹣2,﹣2),(﹣4,﹣1).请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC绕着某点按顺时针方向旋转得到△A′B'C',请直接写出旋转中心的坐标和旋转角度.
(2)画出△ABC关于点A成中心对称的△AED,若△ABC内有一点P(a,b),请直接写出经过这次变换后点P的对称点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
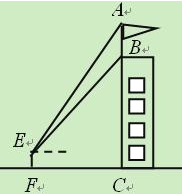
【题目】如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为.6m.
⑴求建筑物BC的高度;
⑵求旗杆AB的高度.(结果精确到0.1m.参考数据:![]() ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系XOY中,二次函数图像的顶点坐标为![]() ,且与x轴的两个交点间的距离为6.
,且与x轴的两个交点间的距离为6.
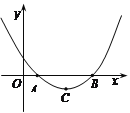
(1)求二次函数解析式;
(2)在x轴上方的抛物线上,是否存在点Q,使得以点Q、A、B为顶点的三角形与△ABC相似?如果存在,请求出Q点的坐标,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com