
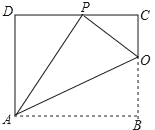
【题目】已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AD的长.
【答案】(1)证明见解析(2)8
【解析】
(1)根据两角对应相等的两个三角形相似即可判定.(2)根据相似三角形的性质面积比等于相似比的平方,得到AD=2PC,设PC=x,则AD=2x,在RT△ADP中利用勾股定理即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°,
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B,
∴∠APO=90°,
∴∠APD=90°﹣∠CPO=∠POC,
∵∠D=∠C,∠APD=∠POC,
∴△OCP∽△PDA.
(2)解:∵△OCP与△PDA的面积比为1:4,
∴![]() =
=![]() =
=![]() ,
,
∴DA=2CP.设PC=x,则AD=2x,PD=10﹣x,AP=AB=10,
在Rt△PDA中,∵∠D=90°,PD 2+AD2=AP2,
∴(10﹣x)2+(2x)2=102,
解得:x=4,
∴AD=2x=8.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,且
,且![]() .
.

(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,

求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要30名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生18人,女生12人.
(1)若从这30人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC>AB.
(1)作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)
(2)在(1)的条件下,若BC=14,求△APQ的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 轴,
轴,![]() 轴,点
轴,点![]() 在x轴上,A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2)把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是()
在x轴上,A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2)把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是()

A.(1,1)B.(1,2)
C.(1,2)D.(1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,易证MN=AM+CN
⑴ 如图2,在梯形ABCD中,BC∥AD,AB=BC=CD, 点M、N分别在AD、CD上,若∠MBN=![]() ∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
⑵ 如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=![]() ∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.
∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com