
【题目】如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,易证MN=AM+CN
⑴ 如图2,在梯形ABCD中,BC∥AD,AB=BC=CD, 点M、N分别在AD、CD上,若∠MBN=![]() ∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
∠ABC ,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
⑵ 如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=![]() ∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.
∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.

【答案】(1)MN=AM+CN,证明见解析(2)MN=CN-AM
【解析】
(1)先判定梯形ABCD是等腰梯形,根据等腰梯形的性质可得∠A+∠BCD=180°,再把△ABM绕点B顺时针旋转90°,点A与点C重合,点M到达点M′,根据旋转变换的性质,△ABM和△CBM′全等,根据全等三角形对应边相等可得AM=CM′,BM=BM′,根据全等三角形对应角相等可得∠A=∠BCM′,∠ABM=∠M′BC,然后证明M′、C、N三点共线,再利用“边角边”证明△BMN和△BM′N全等,然后根据全等三角形对应边相等即可得证;
(2)在∠CBN内部作∠CBM′=∠ABM交CN于点M′,然后证明∠C=∠BAM,再利用“角边角”证明△ABM和△CBM′全等,根据全等三角形对应边相等可得AM=CM′,BM=BM′,再证明∠MBN=∠M′BN,利用“边角边”证明△MBN和△M′BN全等,根据全等三角形对应边相等可得MN=M′N,从而得到MN=CN-AM.
(1)MN=AM+CN.
理由如下:
如图,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=![]() ∠ABC,
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=![]() ∠ABC,
∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
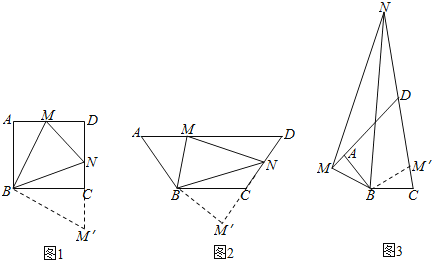
∵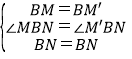 ,
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(2)MN=CN-AM.
理由如下:如图,作∠CBM′=∠ABM交CN于点M′,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠C=360°-180°=180°,
又∵∠BAD+∠BAM=180°,
∴∠C=∠BAM,
在△ABM和△CBM′中,
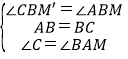 ,
,
∴△ABM≌△CBM′(ASA),
∴AM=CM′,BM=BM′,
∵∠MBN=![]() ∠ABC,
∠ABC,
∴∠M′BN=∠ABC-(∠ABN+∠CBM′)=∠ABC-(∠ABN+∠ABM)=∠ABC-∠MBN=![]() ∠ABC,
∠ABC,
∴∠MBN=∠M′BN,
在△MBN和△M′BN中,
∵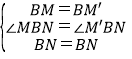 ,
,
∴△MBN≌△M′BN(SAS),
∴MN=M′N,
∵M′N=CN-CM′=CN-AM,
∴MN=CN-AM.


科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 和
和![]() 的正方形如图放置(图1),其未叠合部分(阴影)面积为
的正方形如图放置(图1),其未叠合部分(阴影)面积为![]() ;若再在图1中大正方形的右下角摆放一个边长为
;若再在图1中大正方形的右下角摆放一个边长为![]() 的小正方形(如图2),两个小正方形叠合部分(阴影)面积为
的小正方形(如图2),两个小正方形叠合部分(阴影)面积为![]() .
.



(1)用含![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,求出图3中阴影部分的面积
时,求出图3中阴影部分的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
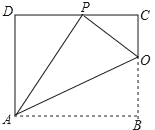
【题目】已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
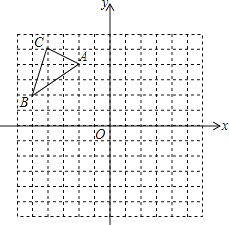
(1)在图中画出平移后的△A1B1C1.
(2)直接写出△A1B1C1.各顶点的坐标:A1____;B1____;C1____.
(3)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上(
上(![]() ,
,![]() 除外),
除外),![]() 的垂线
的垂线![]() 与
与![]() 的垂线
的垂线![]() 交于点
交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
(1)在探究![]() ,
,![]() 的关系时,运用“从特殊到一般”的数学思想,发现当点
的关系时,运用“从特殊到一般”的数学思想,发现当点![]() 是
是![]() 的中点时,只需要取
的中点时,只需要取![]() 边的中点
边的中点![]() (如图),通过推理证明就可以得到
(如图),通过推理证明就可以得到![]() 的数量关系,请你按照这种思路直接写出
的数量关系,请你按照这种思路直接写出![]() 和
和![]() 的数量关系:_____________________
的数量关系:_____________________

(2)当点![]() 是线段
是线段![]() 上(
上(![]() ,
,![]() 除外)任意一点(其它条件不变),上面得到的结论是否仍然成立呢?证明你的结论;
除外)任意一点(其它条件不变),上面得到的结论是否仍然成立呢?证明你的结论;

(3)点![]() 在线段
在线段![]() 的延长线上,上面得到的结论是否仍然成立呢?在下图中画出图形,并证明你的结论.
的延长线上,上面得到的结论是否仍然成立呢?在下图中画出图形,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用因式分解法解下列方程:
(1)(4x﹣1)(5x+7)=0.
(2)3x(x﹣1)=2﹣2x.
(3)(2x+3)2=4(2x+3).
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.

(1)求抛物线的解析式;
(2)在(1)中抛物线的第三象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com