【题目】如图，在平面直角坐标系中，
轴，
轴，点
在x轴上，A（1，2），B（-1，2），D（-3，0），E（-3，-2），G（3，-2）把一条长为2018个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A-B-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（）
A.（1，1）B.（1，2）
C.（1，2）D.（1，0）
科目：初中数学 来源： 题型：
【题目】如图
中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点
若
，
，
，
，则BN的长度为
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
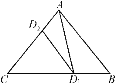
【题目】定义：若经过三角形顶点的一条直线把三角形分割出至少一个图形与原三角形相似，则称这条直线为三角形的自似线，如图，△ABC中，AC＝b，BC＝a，∠C＜∠B＜∠A，过顶点A作∠CAD1＝∠B，交边BC于点D1，依次过顶点D1作∠CD1D2＝∠CAD1，过点D2作∠CD2D3＝∠CD1D2，…，过点Dn－1作∠CDn－1Dn＝∠CDn－2Dn－1.
(1)试证直线AD1是△ABC的自似线；
(2)试求线段CD1的长，并猜想CDn的长；
(3)当60°＜∠A＜120°，且n＝5时，与△ABC相似的三角形有几个？
查看答案和解析>>
科目：初中数学 来源： 题型：
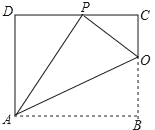
【题目】已知：如图，矩形ABCD的一条边AB=10，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，折痕为AO．
（1）求证：△OCP∽△PDA；
（2）若△OCP与△PDA的面积比为1：4，求边AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D落在AB边上，斜边DE交AC于点F，则n的大小和图中阴影部分的面积分别为（ ）
A. 30，2 B. 60，2 C. 60，
D. 60，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移4个单位长度得到△A1B1C1．（图中每个小方格边长均为1个单位长度）．
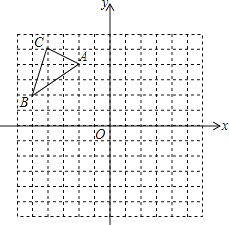
（1）在图中画出平移后的△A1B1C1．
（2）直接写出△A1B1C1．各顶点的坐标：A1____；B1____；C1____．
（3）求出△A1B1C1的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，点
在直线
上（
，
除外），
的垂线
与
的垂线
交于点
，研究和的数量关系.
（1）在探究，的关系时，运用“从特殊到一般”的数学思想，发现当点是的中点时，只需要取
边的中点
（如图），通过推理证明就可以得到
的数量关系，请你按照这种思路直接写出和的数量关系：_____________________
（2）当点是线段上（，除外）任意一点（其它条件不变），上面得到的结论是否仍然成立呢？证明你的结论；
（3）点在线段的延长线上，上面得到的结论是否仍然成立呢？在下图中画出图形，并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y=kx+6与抛物线y=ax2+bx+c相交于A，B两点，且点A（1，4）为抛物线的顶点，点B在x轴上．
（1）求抛物线的解析式；
（2）在（1）中抛物线的第三象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；
（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中,∠C=90°，⊙I为△ABC的内切圆，点O为△ABC的外心，BC=6，AC=8．
（1）求⊙I的半径；
（2）求线段OI的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
