
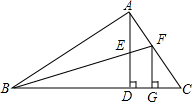
 如图,已知△ABC中,∠BAC=90°,AD⊥BC于D,E是AD的中点,BE的延长线交AC于F,FG⊥BC于G.求证:$\frac{FG}{AF}$=$\frac{CF}{FG}$.
如图,已知△ABC中,∠BAC=90°,AD⊥BC于D,E是AD的中点,BE的延长线交AC于F,FG⊥BC于G.求证:$\frac{FG}{AF}$=$\frac{CF}{FG}$. 分析 延长BA,GF相交于点H,可得到△HAF∽△CGF,由相似三角形的性质得到$\frac{AE}{FH}$=$\frac{GE}{GF}$,即AF•CF=FG•HF,然后只要证明FG=HF即可.
解答 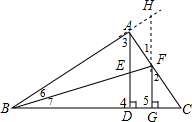 证明:延长BA,GF相交于点H,
证明:延长BA,GF相交于点H,
∵FG⊥BC,
∴∠FGC=90°.
∵∠ACB=90°,∴∠FGC=∠BCC,
∵∠1=∠2,
∴△HAF∽△CGF,
∴$\frac{AF}{FG}$=$\frac{HF}{CF}$,即AF•CF=FG•HF,
∵AD⊥BC,FG⊥BC,
∴∠4=∠5=90°,
∴AD∥HG,
∴∠3=∠H,
∵∠3=∠H,∠6=∠6,
∴△ABE∽△BHF,
∴$\frac{BE}{BF}$=$\frac{AE}{FH}$,
∵∠4=∠5,∠7=∠7
∴△BED∽△BFG,
∴$\frac{BE}{BF}$=$\frac{GE}{GF}$,
∴$\frac{AE}{FH}$=$\frac{GE}{GF}$,
∵E是CD的中点,
∴AE=DE,
∴FH=FG,
∵AF•CF=FG•HF,
∴CF•BF=FG•FG
∴$\frac{FG}{AF}$=$\frac{CF}{FG}$.
点评 本题主要考查了相似三角形的判定方法与性质,比例的性质,正确的作出辅助线是解题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 每个内角都是120°的六边形一定是正六边形 | |
| B. | 正n边形的对称轴不一定有n条 | |
| C. | 正n边形的每一个外角度数等于它的中心角度数 | |
| D. | 正多边形一定既是轴对称图形,又是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
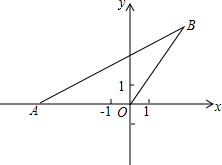 已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=$\frac{1}{2}$
已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=$\frac{1}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
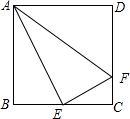 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 差值/g | -4.5 | +5 | 0 | +5 | 0 | 0 | +2 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
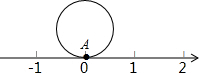 如图所示,把半径为1个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达A′的位置,则点A′表示的数是-6.(π取3)
如图所示,把半径为1个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达A′的位置,则点A′表示的数是-6.(π取3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com