
Ϊ���˽�ѧ����ע�ȵ����ŵ�����������ᡱ�ڼ䣬С���༶ͬѧһ�����տ������ᡱ���ŵĴ���������˵��飬������ͳ����ͼ��ʾ�����������տ�3�ε�����û�б����������������Ϣ��������и��⣺
��1���ð༶Ů����������������������Ů���տ������ᡱ���Ŵ���������������������������λ������������������
��2����Ů���տ�������ƽ������
��3��Ϊ��һ�������ð༶�С�Ů���տ������ᡱ���Ŵ������ص㣬С�������Ů���տ������ᡱ���Ŵ����ķ���Ϊ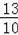
 �������տ������ᡱ���Ŵ����ķ���Ϊ2����Ƚϸð༶�С�Ů���տ������ᡱ���Ŵ����IJ�����С��
�������տ������ᡱ���Ŵ����ķ���Ϊ2����Ƚϸð༶�С�Ů���տ������ᡱ���Ŵ����IJ�����С��
��4������ij��Ⱥ�壬���ǰ�һ�����տ�ij�ȵ����Ŵ���������3�ε�����ռ������Ⱥ���������İٷֱȽ�����Ⱥ���ij�ȵ����ŵġ���עָ����������ð༶�����ԡ����ᡱ���ŵġ���עָ������Ů����5%������ð༶����������
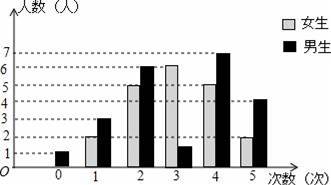
��
�����㡿����ͳ��ͼ�����ʽ���̣���Ȩƽ��������λ�������������
��ר�⡿�����⣻����˼�룻ͳ�Ƶ�Ӧ�ã�
����������1�������ۿ�������������ӵõ�Ů���������ۿ���������Ϊ��������С�������к����м���м�������ƽ��Ϊ��λ����
��2�����ݼ�Ȩƽ�������㷨����ʽ���㼴�ɣ�
��3���ɷ�����жϣ�����С˵������С��
��4���������⣬���Ů���Ĺ�עָ���������õ������Ĺ�עָ��������������Ϊx���г����̣���֮�ɵã�
����𡿽⣺��1���ð༶Ů������Ϊ��2+5+6+5+2=20���ˣ���
�����տ�3�ε�������࣬��6�Σ�������Ϊ3��
�ð༶Ů���տ���������λ���Ǵ�С�������еĵ�10��11������ƽ��������Ϊ3������λ����3��
��2��Ů���տ�������ƽ�����ǣ�
 ����1��2+2��5+3��6+4��5+5��2��=
����1��2+2��5+3��6+4��5+5��2��=
 =30��
=30��
��3����2��
 ��
��
������������Ů���IJ������ȴ�
��4�������⣺�ð�Ů���ԡ����ᡱ���ŵġ���עָ����Ϊ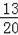
 ��100%=65%��
��100%=65%��
���ԣ������ԡ����ᡱ���ŵġ���עָ����Ϊ60%
��������x��
��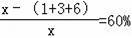
 ��
��
��ã�x=25��
�𣺸ð༶������25�ˣ�
���������������������ͳ�Ʊ��л�ȡ�������ݵ����������û�ȡ�����ݽ��м��㡢����������������ȡ��������ʱ����ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����и���ֵ�����߶εij��ȣ�����������ε���( )
A��1��2��3.5 B��4��5��9 C��5��15��8 D��20��15��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���������·����ָ�Ӳ���Ҫ��ij·�ι��̽����б꣬�ӵ��˼ס����������̶ӵ�Ͷ���飮��Ͷ�����е�֪���ӵ����������������������Ҷӵ���������������������
 �����ɼ�����10�죬ʣ�µĹ������ɼס������Ӻ���30����ɣ�
�����ɼ�����10�죬ʣ�µĹ������ɼס������Ӻ���30����ɣ�
��1����ס������ӵ����������̸�������죿
��2����֪��ÿ���ʩ������Ϊ8.4��Ԫ���Ҷ�ÿ���ʩ������Ϊ5.6��Ԫ������Ԥ���ʩ������Ϊ500��Ԫ��Ϊ���̹��ڲ���Ч��ɹ��̣��ⰲ��Ԥ���ʩ�������Ƿ��ã��������ã�����Ԥ�������Ԫ�����������жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������y=
 ��ͼ����A��1����3����AB��ֱx���ڵ�B��������˵����ȷ���ǣ�������
��ͼ����A��1����3����AB��ֱx���ڵ�B��������˵����ȷ���ǣ�������


A��k=3 B��x��0ʱ��y��x���������
C��S��AOB=3 D������ͼ�����y��Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��������ABCDEF�ڽ��ڡ�O��ͼ����Ӱ���ֵ����Ϊ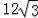
 �����O�İ뾶Ϊ��������������
�����O�İ뾶Ϊ��������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
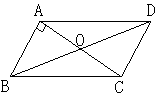
��ͼ��ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB��AC��AB=4��AC=6��
��BD�ij��� ��
A��8 B��9 C��10 D��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������⣬���ʺ���ȫ�������ǣ�������
A���˽�ȫ��ͬѧÿ������������ʱ��
B���ÿ��Ϸɻ�ǰ�İ���
C��ѧУ��Ƹ��ʦ����ӦƸ��Ա����
D���˽�ȫ����Сѧ��ÿ����㻨Ǯ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�Ļ��̳�ͬʱ������̨�����٣�ÿ̨����960Ԫ���Գɱ����㣬��һ̨ӯ��20%����һ̨����20%���γ����У��̳���������
A�������� B��160Ԫ C��80Ԫ D����80Ԫ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com