
 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$. 分析 先根据等腰三角形的性质求出∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1,∠B2A3A2及∠B3A4A3的度数,找出规律即可得出∠A2015A2016B2015的度数.
解答 解:∵在△ABA1中,∠B=20°,AB=A1B,
∴∠BA1A=$\frac{180°-∠B}{2}$=80°,
∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,
∴∠B1A2A1=$\frac{∠B{A}_{1}A}{2}$=40°;
同理可得,
∠B2A3A2=20°,∠B3A4A3=10°,
∴∠An-1AnBn-1=$\frac{80°}{{2}^{n-1}}$,
∴∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
故答案为:$\frac{80°}{{2}^{2015}}$.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠B1C2A1,∠B2A3A2及∠B3A4A3的度数,找出规律是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
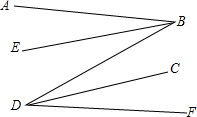 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com