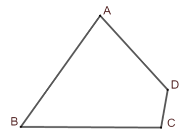
【题目】如图，四边形ABCD中，∠ABC 60，∠ADC 120，AB BC，AD DC 2，则四边形ABCD的面积是__________．
【答案】
【解析】
由题意正确作出辅助线并根据等边三角形判定与性质和全等三角形的判定和性质以及勾股定理进行综合分析求解.
解：如图，延长CD至E，使DE=DA．连接AC．
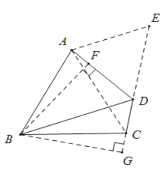
∵∠ADC=120°，
∴∠ADE=60°，
∵AD=DE，
∴△EAD是等边三角形，
∴AE=AD，∠DAE=60°，
∵AB=AC，∠ABD=60°，
∵∠BAD=60°+∠CAD，∠EAC=60°+∠CAD，
∴∠BAD=∠CAE，
∴△BAD≌△CAE（SAS），
故AD+CD=DE+CD=CE=BD=2．
∴∠ADB=∠E=60°，
∴∠BDC=120°-60°=60°，
过点B作BF⊥AD于F点，过B点作BG⊥DC，交DC延长线于G点，
在Rt△BFD中，DF=
BD=1，由勾股定理可得BF=，
同理可得BG=．
四边形ABCD面积=△ABD面积+△BCD面积= ADBF+CDBG=（AD+CD），
∵AD DC 2，
∴四边形ABCD面积=
=．
故答案为：．
世纪百通期末金卷系列答案科目：初中数学 来源： 题型：
【题目】攀枝花得天独厚，气候宜人，农产品资源极为丰富，其中晚熟芒果远销北上广等大城市．某水果店购进一批优质晚熟芒果，进价为10元/千克，售价不低于15元/千克，且不超过40元/每千克，根据销售情况，发现该芒果在一天内的销售量
（千克）与该天的售价
（元/千克）之间的数量满足如下表所示的一次函数关系．
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
（1）某天这种芒果售价为28元/千克．求当天该芒果的销售量
（2）设某天销售这种芒果获利
元，写出与售价之间的函数关系式．如果水果店该天获利400元，那么这天芒果的售价为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，A，B两个顶点在x轴上方，点C的坐标是(﹣1，0)，以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，得到△A'B'C'，设点B的对应点B'的横坐标为2，则点B的横坐标为( )
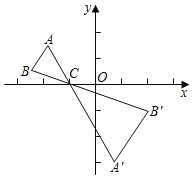
A.﹣1B.
C.﹣2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
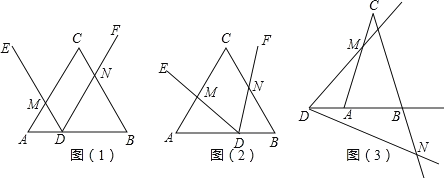
【题目】已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A，B重合)，DE交AC所在直线于点M，DF交BC所在直线于点N，设AM=x，BN=y，记△ADM的面积为S1，△BND的面积为S2．
（1）如图（1），当△ABC是等边三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2时，S1S2= ；
（2）在（1）的条件下，将点D沿AB平移，使AD=4，再将∠EDF绕点D旋转如图（2）所示位置，
①求y与x的函数关系式；②求S1S2的值；
（3）当△ABC是等腰三角形时，设∠B=∠A=∠EDF=α，如图（3），当点D在BA的延长线上运动时，设的AD=a，BD=b，直接写出S1S2的关系式(用含a、b和α的三角函数表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，C为⊙O上一点，∠CAB的角平分线AD交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线；
（2）若∠CAB=60°，DE=3
，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，AB＝AC，∠BAC＝120°，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．
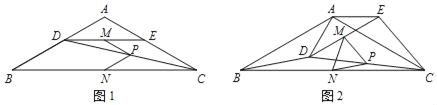
（1）观察猜想
图1中，线段PM与PN的数量关系是 ，∠MPN的度数是 ；
（2）探究证明
把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；
（3）拓展延伸
把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝8，请直接写出△PMN面积的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着经济的快速发展，环境问题越来越受到人们的关注．某校学生会为了了解垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，并将调查结果绘制成下面两幅统计图．
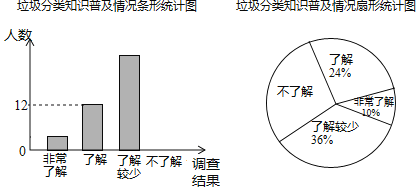
（1）求：本次被调查的学生有多少名？补全条形统计图．
（2）估计该校1200名学生中“非常了解”与“了解”的人数和是多少．
（3）被调查的“非常了解”的学生中有2名男生，其余为女生，从中随机抽取2人在全校做垃圾分类知识交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系 XOY中，对于任意两点 
(
,
)与 
(,
)的“非常距离”，给出如下定义： 若 
，则点 与点 的“非常距离”为 
；若 
，则点 与点的“非常距离”为 
.
例如：点 (1,2)，点 (3,5)，因为 
，所以点 与点 的“非常距离”为 
，也就是图1中线段 Q与线段 Q长度的较大值（点 Q为垂直于 y轴的直线 Q与垂直于 x轴的直线 Q的交点）。
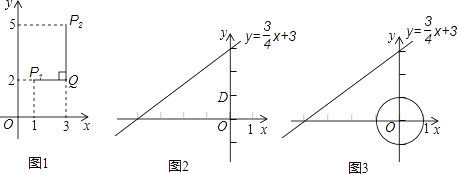
（1）已知点 A(-
,0)， B为 y轴上的一个动点，①若点 A与点 B的“非常距离”为2，写出一个满足条件的点 B的坐标；②直接写出点 A与点 B的“非常距离”的最小值；
（2）已知 C是直线 
上的一个动点，①如图2，点 D的坐标是（0，1），求点 C与点 D的“非常距离”的最小值及相应的点 C的坐标； ②如图3， E是以原点 O为圆心，1为半径的圆上的一个动点，求点 C与点 E的“非常距离”的最小值及相应的点 E和点 C的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
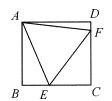
【题目】如图，在矩形 ABCD 中，点 E，F 分别在 BC，CD 边上，且 CE＝3，CF＝4.若△AEF 是等边三角形，则 AB 的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com