
【题目】如图,![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 厘米,
厘米,![]() ,
,![]() 厘米.若点
厘米.若点![]() 在线段
在线段![]() 上以每秒3厘米的速度从点
上以每秒3厘米的速度从点![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 在线段
在线段![]() 上从点
上从点![]() 向终点
向终点![]() 运动.
运动.

(1)若点![]() 的速度与点
的速度与点![]() 的速度相等,经1秒钟后,请说明
的速度相等,经1秒钟后,请说明![]() ;
;
(2)若点![]() 的速度与点
的速度与点![]() 的速度不相等,当点
的速度不相等,当点![]() 的速度为多少时,能够使
的速度为多少时,能够使![]() .
.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的角平分线OC上的任意一点.
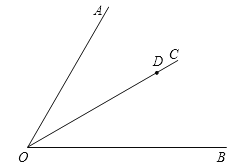
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OC,垂足为点D,DF与OB交于点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于_____mm(精确到1mm);
(2)在(1)所画出的图形中,若∠AOB=n,则∠EDF=____________度(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
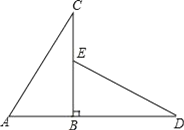
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
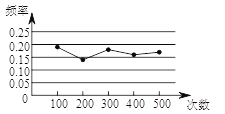
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=-2x+5 的图像分别与 x 轴,y 轴交于点A、B,以线段AB 为边在第一象限内作等腰 RtABC,BAC=90 ,求过 B、C 两点的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)求值:![]()
(2)用消元法解方程组 时,两位同学的解法如下:
时,两位同学的解法如下:
解法一:
由①-②,得![]() .
.
解法二:
由②得,![]() ,③
,③
把①代入③,得![]() .
.
①反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
②请选择一种你喜欢的方法,完成解答.
(3)求不等式组 的正整数解.
的正整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现将线段
,现将线段![]() 向上平移
向上平移![]() 个单位, 得到对应线段
个单位, 得到对应线段![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 作匀速 移动,点
作匀速 移动,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 作匀速运动,点
作匀速运动,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为
匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为![]() 秒。在移动过程 中.若
秒。在移动过程 中.若![]() 与
与![]() 全等,则此时的移动时间
全等,则此时的移动时间![]() 的值为____
的值为____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com