
分析 首先,根据$\sqrt{3cosA-2}$+|3-5sinB|=0,得到cosA=$\frac{2}{3}$,sinB=$\frac{3}{5}$,然后,结合同角三角函数基本关系式求解即可.
解答 解:∵$\sqrt{3cosA-2}$≥0,|3-5sinB|≥0,
∴$\sqrt{3cosA-2}$=0,|3-5sinB|=0,
∴3cosA-2=0,5sinB-3=0,
∴cosA=$\frac{2}{3}$,sinB=$\frac{3}{5}$,
∵在△ABC中,
∴sinA=$\sqrt{1-{cos}^{2}A}$=$\sqrt{1-\frac{4}{9}}$=$\frac{\sqrt{5}}{3}$,
∵cosA=$\frac{2}{3}$,sinB=$\frac{3}{5}$,
∴$\frac{π}{4}$<A<$\frac{π}{3}$,$\frac{π}{6}$<B<$\frac{π}{4}$或$\frac{3π}{4}$<B<$\frac{5π}{6}$(舍)
∴cosB=$\sqrt{1-{sin}^{2}B}$=$\frac{4}{5}$.
∴tanA=$\frac{\sqrt{5}}{2}$,cotA=$\frac{2\sqrt{5}}{5}$,tanB=$\frac{3}{4}$,cotB=$\frac{4}{3}$.
点评 本题考查的是解直角三角形,重点考查了三角函数的基本关系,三角形的性质等知识,属于中档题.


科目:初中数学 来源: 题型:解答题
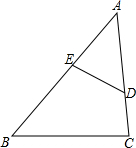 如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°
如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个相等的实数根 | B. | 有两个不等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com