
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y����x2+2|x|+1��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | ��2 | �� | m | 2 | 1 | 2 | 1 | �� | ��2 | �� |
����m���� ����
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
��3���۲캯��ͼ��д���������������ʣ�
��4����һ��̽������ͼ���֣�
�����̩�x2+2|x|+1��0���� ����ʵ������
������x�ķ��̩�x2+2|x|+1��a��4��ʵ����ʱ��a��ȡֵ��Χ���� ����
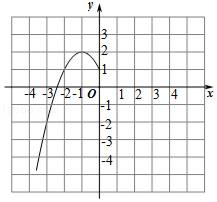
���𰸡���1��1����2�������������3�������������ֵ��2��û����Сֵ������x��1ʱ��y��x���������С����4����2����1��a��2��
��������
��1�����ݶԳƿɵ�m=1��
��2������ͼ�Σ�
��3����д���������ֵ����Сֵ���⣻
��ȷ��һ����Χд���������⣻
��4���ٵ�y=0ʱ����x��Ľ���������������2��ʵ������
�ڵ�y=aʱ����4��ʵ����������4�����㣬ȷ����a��ֵ���ɣ�
�⣺��1���ɱ����֪��ͼ��ĶԳ�����y�ᣬ
��m��1��
�ʴ�Ϊ��1��
��2����ͼ��ʾ��
��3�����ʣ������������ֵ��2��û����Сֵ��
����x��1ʱ��y��x���������С��
��4������ͼ��ã���������x������������
��̩�x2+2|x|+1��0��2��ʵ������
�ʴ�Ϊ��2��
����ͼ���֪����x2+2|x|+1��a��4��ʵ����ʱ��
��y��aʱ����ͼ����4�����㣬
����a��ȡֵ��Χ�ǣ�1��a��2��
�ʴ�Ϊ��1��a��2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����10��10�����������У�ÿ��С�����εı߳���Ϊ1����λ������ABC����ƽ��4����λ���õ���A��B��C�����ٰ���A��B��C���Ƶ�C'˳ʱ����ת90�����õ���A��B��C�������㻭����A��B��C������A��B��C�������![]() �ij���
�ij���
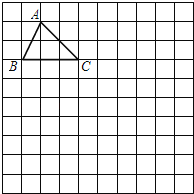
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��x�ύ�ڵ�A(��1��0)������������(1��n)����y��Ľ�����(0��3)��(0��6)֮��(�����˵�)�������н��۴������( )
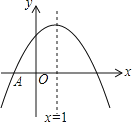
A.3a+b��0B.��2��a����lC.abc��0D.9a+3b+2c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCDΪ�����Σ���A������Ϊ��0��3������B������Ϊ��0����4����������������y��![]() ��k��0����ͼ����C��
��k��0����ͼ����C��
��1�����������Ľ���ʽ��
��2����P�Ƿ����������ڵڶ�����ͼ���ϵ�һ�㣬����PBC���������������ABCD����������P�����꣮
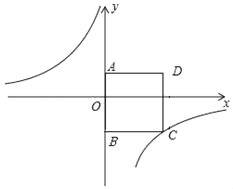
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������AOB�У���AOB=120�㣬OA=2������AΪԲ�ģ�OA��Ϊ�뾶��������AB�ڵ�C������C��CD��OA������ΪD����ͼ����Ӱ���ֵ����Ϊ_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͼ��������ABCD�ı߳�Ϊ3cm������P��B�������3cm/s���ٶ����ű�BC��CD��DA�˶�������A��ֹͣ�˶�����һ����Qͬʱ��B���������1cm/s���ٶ����ű�BA��A���˶�������A��ֹͣ�˶�����P���˶�ʱ��Ϊx��s������BPQ�����Ϊy��cm2������y����x�ĺ���ͼ���ǣ� ��
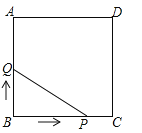
A��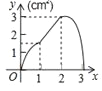 B��
B��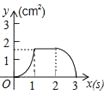 C��
C��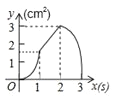 D��
D��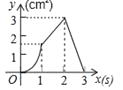
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
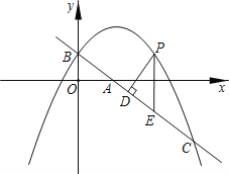
����Ŀ����ͼ��ֱ��y=-![]() x+1��x�ᣮy��ֱ���A��B���㣬������y=-
x+1��x�ᣮy��ֱ���A��B���㣬������y=-![]() x2+bx+c������B������ֱ��AB����һ����ΪC��4��n����
x2+bx+c������B������ֱ��AB����һ����ΪC��4��n����
��1����n��ֵ��������������Ӧ�ĺ�����ϵʽ��
��2�����������ϵ�һ������P�ĺ�����Ϊt��0��t��4��������P��PD��AB�ڵ�D����PE��y�ύֱ��AB�ڵ�E��
��y���ϴ��ڵ�Q��ʹ���ı���QEPB�Ǿ��Σ��������Q�����ꣻ
�����߶�PD�ij������ֵ��
�۵�tΪ��ֵʱ����DΪBE���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC����O����ABC�����Բ��S��ABC��32��BC��8��
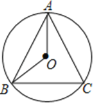
��1�������O�İ뾶r��
��2����S��ABO��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com