
����Ŀ����ͼ��������y=ax2+bx+2��x����A����1��0����B��4��0�����㣬��y���ڵ�C�������C��ƽ����x���ֱ�߽�����һ��D����P����������һ���㣮
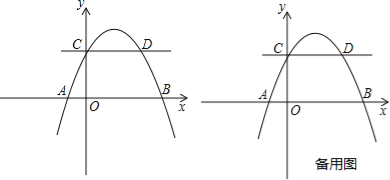
��1���������߽���ʽ����D���ꣻ
��2����E��x���ϣ�����A��E��D��PΪ������ı�����ƽ���ı��Σ����ʱ��P�����ꣻ
��3������P��ֱ��CD�Ĵ��ߣ�����ΪQ��������CPQ��CP���ۣ���Q�Ķ�Ӧ��ΪQ�����Ƿ���ڵ�P��ʹQ��ǡ������x���ϣ������ڣ������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��![]() ����D����Ϊ��3��2����2��P1��0��2����P2��
����D������3��2����2��P1��0��2����P2��![]() ����2����P3��
����2����P3��![]() ����2����3�����ڣ���
����2����3�����ڣ���![]() ������
������![]() ��
��
��������
�⣺��1����������y=ax2+bx+2����A����1��0����B��4��0�����㣬
��![]() ����ã�
����ã�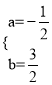 ��
��
�������߽���ʽΪ![]() ��
��
��y=2ʱ��![]() ����ã�x1=3��x2=0����ȥ����
����ã�x1=3��x2=0����ȥ����
����D������3��2����
��2��A��E���㶼��x���ϣ�AE�����ֿ��ܣ�
����AEΪһ��ʱ��AE��PD����P1��0��2����
����AEΪ�Խ���ʱ������ƽ���ı��ζԶ��㵽��һ���Խ��߾�����ȣ���֪P�㡢D�㵽ֱ��AE����x�ᣩ�ľ�����ȣ���P���������Ϊ��2��
���������ߵĽ���ʽ��![]() ����ã�
����ã�![]() ��
��
��P���������![]() ����2������
����2������![]() ����2����
����2����
����������P1��0��2����P2��![]() ����2����P3��
����2����P3��![]() ����2����
����2����
��3���������������ĵ�P����Ȼ��P��ֱ��CD�·���
��ֱ��PQ��x����F����P������Ϊ��![]() ����
����
����P����y���Ҳ�ʱ����ͼ1����CQ=a��
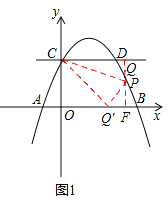
PQ=![]() ��
��
���ߡ�CQ��O+��FQ��P=90������COQ��=��Q��FP=90����
���FQ��P=��OCQ�������COQ��ס�Q��FP��
��![]() ����
����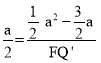 �����F Q��=a��3
�����F Q��=a��3
��OQ��=OF��F Q��=a����a��3��=3��
![]() ��
��
��ʱa=![]() ����P������Ϊ��
����P��������![]() ����
����
����P����y�����ʱ����ͼ2����ʱa��0����![]() ��0��CQ=��a������ͼ��
��0��CQ=��a������ͼ��
PQ=![]() ��
��
���ߡ�CQ��O+��FQ��P=90������CQ��O+��OCQ��=90����
���FQ��P=��OCQ������COQ��=��Q��FP=90����
���COQ��ס�Q��FP��
��![]() ����
����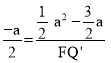 �����F Q��=3��a��
�����F Q��=3��a��
��OQ��=3��![]() ��
��
��ʱa=��![]() ����P������Ϊ��
����P��������![]() ����
����
�������������������ĵ�P����Ϊ��![]() ������
������![]() ����
����
��1���ô���ϵ�����ɵó������ߵĽ���ʽ����y=2�ɵó���D�����꣮
��2������������������ۣ�����AEΪһ��ʱ��AE��PD������AEΪ�Խ���ʱ������ƽ���ı��ζԶ��㵽��һ���Խ��߾�����ȣ�����P���꣮
��3�����ͼ�ο��жϳ���P��ֱ��CD�·������P������Ϊ��![]() ������������ۣ�����P����y���Ҳ�ʱ������P����y�����ʱ�����ý�ֱ�������μ����������ε����ʽ�����⼴�ɣ�
������������ۣ�����P����y���Ҳ�ʱ������P����y�����ʱ�����ý�ֱ�������μ����������ε����ʽ�����⼴�ɣ�


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
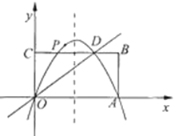
����Ŀ������OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA(6��0)��C(0��3)��ֱ��y=![]() x��BC���ཻ��D��
x��BC���ཻ��D��
��1�����D�����꣺
��2����������y=ax![]() ��bx����D��A���㣬��ȷ���������ߵı���ʽ��
��bx����D��A���㣬��ȷ���������ߵı���ʽ��
��3��PΪx���Ϸ���2�����е���������һ�㣬���POA��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
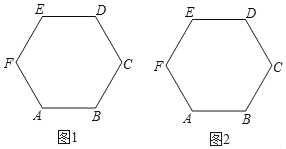
����Ŀ����������ABCDEF�ı߳�1��������̶ȵ�ֱ�߰�Ҫ��ͼ��
��1����ͼ1�У�����һ������Ϊ![]() ���߶Σ�
���߶Σ�
��2����ͼ2�У�����һ������Ϊ![]() ���߶Σ���˵�����ɣ�
���߶Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ��������O����AD�Ĵ��߽���ԲO�ڵ�E����AC�ڵ�C��ʹ��BED=��C��
��1���ж�ֱ��AC��ԲO��λ�ù�ϵ����֤����Ľ��ۣ�
��2����AC=8��cos��BED=![]() ����AD�ij���
����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��5�£��ԡ�Ѱ����ѧ������������Ϊ����������е����조��ѧ����ǿһ��ѧ֪ʶ��ս�����ܾ��������Ļ��С���������ܾ���.�������̷��������ڣ�����ѡ������ÿ�������и�ѡ��һ����Ŀ.
��һ���ڣ�д��ע����������¡���ѧ��ʶ������������ֱ���![]() ��ʾ����
��ʾ����
�ڶ����ڣ�������д��ʫ�ʶԾ䡢����ͨ�����ֱ���![]() ��ʾ��
��ʾ��
��1��������״ͼ���б��ķ�����ʾС���μ��ܾ�����ȡ��Ŀ�����п��ܽ��
��2����С���μ��ܾ�����ȡ��Ŀ���dz�����Ŀ��������¡����������������д���ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����![]() ��ͼ��G������
��ͼ��G������![]() ��ֱ��
��ֱ��![]() ��y�ύ�ڵ�B����ͼ��G���ڵ�C.
��y�ύ�ڵ�B����ͼ��G���ڵ�C.
��1����m��ֵ.
��2���ᡢ�����궼�������ĵ��������.��ͼ��G�ڵ�A��C֮��IJ������߶�BA��BCΧ�ɵ��������߽磩ΪW.
�ٵ�ֱ��l����![]() ʱ��ֱ��д������W�ڵ��������.
ʱ��ֱ��д������W�ڵ��������.
��������W�ڵ����㲻����4������Ϻ���ͼ����k��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У��Խ���
�У��Խ���![]() �Ĵ�ֱƽ���߽�ֱ��
�Ĵ�ֱƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��Ϊ______��
��Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ�����֪���߶μ�һ�������������ij߹���ͼ����.
��֪���߶�![]() ��
��![]() ����O .
����O .

��������ABC��ʹ���߶�![]() ��
��![]() ����O�ֱ����������ߺ�һ��.
����O�ֱ����������ߺ�һ��.
��������ͼ,
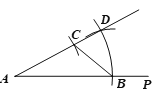
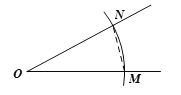
���Ե�OΪԲ�ģ�![]() ��Ϊ�뾶�������ֱ�O�������ڵ�M ,N��
��Ϊ�뾶�������ֱ�O�������ڵ�M ,N��
�ڻ�һ������AP���Ե�AΪԲ�ģ�![]() ��Ϊ�뾶��������AP�ڵ�B��
��Ϊ�뾶��������AP�ڵ�B��
���Ե�BΪԲ�ģ�MN��Ϊ�뾶��������ڢڲ��������Ļ��ཻ�ڵ�D��
�ܻ�����AD��
���Ե�AΪԲ�ģ�![]() ��Ϊ�뾶��������AD�ڵ�C��
��Ϊ�뾶��������AD�ڵ�C��
������BC ������ABC����������������.
��ش�:
��1������۵õ������߶���ȣ��� = ��
��2����A����O����ͼ������ ��
��3��С��˵С������ͼ��ȫ�棬ԭ���� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() �r
�r![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��ֱ��
��ֱ��![]() ��
��
(1)��![]() ʱ������ֱ��
ʱ������ֱ��![]() ��������
��������![]() ����ֱ��д��ֱ��
����ֱ��д��ֱ��![]() ��������
��������![]() �صõ��߶γ���
�صõ��߶γ���
(2)����![]() ȡֵ�ı仯���жϵ�
ȡֵ�ı仯���жϵ�![]() �Ƿ���ֱ��
�Ƿ���ֱ��![]() �ϲ�˵�����ɣ�
�ϲ�˵�����ɣ�
(3)��ֱ��![]() ��������
��������![]() �صõ��߶γ���С��3����Ϻ�����ͼ��ֱ��д��
�صõ��߶γ���С��3����Ϻ�����ͼ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com