
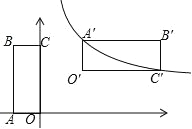
【题目】如图,在平面直角坐标系中,矩形 OABC 的边 OA 与 x 轴重合,B 的坐标为(﹣1,2),将矩形 OABC 绕平面内一点 P 顺时针旋转 90°,使 A、C 两点恰好落在反比例函数 y=![]() 的图象上,则旋转中心 P 点的坐标是( )
的图象上,则旋转中心 P 点的坐标是( )
A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
【答案】C
【解析】
设 A'(a,![]() ),则 C'(a+2,
),则 C'(a+2,![]() ﹣1),依据反比例函数图象上点的坐标特征,即可得到 a=2,进而得出 A'(2,2),C'(4,1),设 P(x,y),再根据 AP=A'P,CP=C'P,即可得到方程组
﹣1),依据反比例函数图象上点的坐标特征,即可得到 a=2,进而得出 A'(2,2),C'(4,1),设 P(x,y),再根据 AP=A'P,CP=C'P,即可得到方程组![]() ,进而得出旋转中心 P 点的坐标.
,进而得出旋转中心 P 点的坐标.
如图,∵B 的坐标为(﹣1,2),
∴矩形的长为 2,宽为 1,
由旋转可得,A'O'⊥x 轴,O'C'⊥y 轴,
设 A'(a,![]() ),则 C'(a+2,
),则 C'(a+2,![]() ﹣1),
﹣1),
∵点 C'在反比例函数 y=![]() 的图象上,
的图象上,
∴(a+2)(![]() ﹣1)=4,解得 a=2(负值已舍去),
﹣1)=4,解得 a=2(负值已舍去),
∴A'(2,2),C'(4,1),
由旋转的性质可得,AP=A'P,CP=C'P, 设 P(x,y),
则![]() ,
,
解得![]() ,
,
∴旋转中心 P 点的坐标是(![]() ,﹣
,﹣![]() ),故选:C.
),故选:C.


科目:初中数学 来源: 题型:
【题目】如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为![]() cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.

(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是180m2的无盖长方体纸盒,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
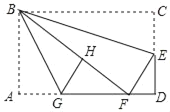
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=2x+4与两坐标轴分别交于A,B两点.
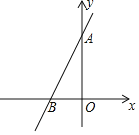
(1)若一次函数y=﹣![]() x+m与直线AB的交点在第二象限,求m的取值范围;
x+m与直线AB的交点在第二象限,求m的取值范围;
(2)若M是y轴上一点,N是x轴上一点,直线AB上是否存在两点P,Q,使得以M,N,P,Q四点为顶点的四边形是正方形.若存在,求出M,N两点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
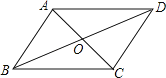
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
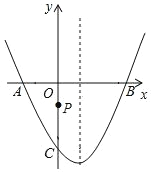
【题目】如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象交 x 轴于A、B 两点,交 y 轴于 C 点,P 为 y 轴上的一个动点,已知 A(﹣2,0)、C(0,﹣2![]() ),且抛物线的对称轴是直线 x=1.
),且抛物线的对称轴是直线 x=1.
(1)求此二次函数的解析式;
(2)连接 PB,则 ![]() PC+PB 的最小值是 ;
PC+PB 的最小值是 ;
(3)连接 PA、PB,P 点运动到何处时,使得∠APB=60°,请求出 P 点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益民商店经销某种商品,进价为每件80元,商店销售该商品每件售价高干8元且不超过120元若售价定为每件120元时,每天可销售200件,市场调查反映:该商品售价在120元的基础上,每降价1元,每天可多销售10件,设该商品的售价为![]() 元,每天销售该商品的数量为
元,每天销售该商品的数量为![]() 件.
件.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)商店在销售该商品时,除成本外每天还需支付其余各种费用1000元,益民商店在某一天销售该商品时共获利8000元,求这一天该商品的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com