
【题目】在平面直角坐标系中,直线y=2x+4与两坐标轴分别交于A,B两点.
(1)若一次函数y=﹣![]() x+m与直线AB的交点在第二象限,求m的取值范围;
x+m与直线AB的交点在第二象限,求m的取值范围;
(2)若M是y轴上一点,N是x轴上一点,直线AB上是否存在两点P,Q,使得以M,N,P,Q四点为顶点的四边形是正方形.若存在,求出M,N两点的坐标,若不存在,请说明理由.
【答案】(1)m<4;(2)M(0,![]() ),N(﹣
),N(﹣![]() ,0)或M(0,﹣
,0)或M(0,﹣![]() ),N(
),N(![]() ,0)或M(0,﹣4),N(﹣
,0)或M(0,﹣4),N(﹣![]() ,0);
,0);
【解析】
(1)根据题意联立一次函数解析式与直线AB的解析式,据此进一步用![]() 表示出
表示出![]() ,最后根据第二象限的点的坐标特征加以分析即可;
,最后根据第二象限的点的坐标特征加以分析即可;
(2)首先求出A、B两点坐标,然后根据题意分图1、图2、图3共三种情况结合相似三角形性质进一步分析求解即可.
(1)联立![]() 与
与![]() ,得:
,得:![]() ,
,
∴![]() ,
,
∵交点位于第二象限,
∴![]() ,
,
∴![]() ;
;
(2)当![]() 时,
时,![]() ,
,
∴A(0,4),
当![]() 时,
时,![]() ,即:
,即:![]() ,
,
∴B(![]() ,0),
,0),
∴OA=4,OB=2.

如图1,过点Q作QH⊥![]() 轴于H,
轴于H,
∵MN∥AB,
∴△NMO~△BAO,
∴![]() ,
,
设ON=![]() ,则OM=
,则OM=![]() ,
,
∵∠MNQ=90°,
∴∠QNH+∠MNO=∠MNO+∠NMO=90°,
∴∠QNH=∠NMO,
在△QNH和△NMO中,
∵∠QNH=∠NMO,∠QHN=∠NOM,QN=MN,
∴△QNH△NMO(AAS),
∴QH=ON=![]() ,HN=OM=2
,HN=OM=2![]() ,
,
易得:△BQH~△BAO,
∴![]() ,
,
∴BH=![]() ,
,
∵OB=BH+HN+ON,
∴2=![]() ,解得
,解得![]() ,
,
∴M(0,![]() ),N(
),N(![]() ,0);
,0);
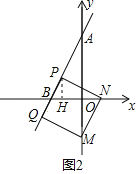
如图2,过点P作PH⊥![]() 轴于H,
轴于H,
易证△PNH~△BAO,
∴![]() ,
,
设PH=b,则NH=2b,
同理证得△PNH△NMO,
∴PH=ON=b,HN=OM=2b,
∴OH=HNOH=b,
易得:△BPH~△BAO,
∴![]() ,
,
∴BH=![]() b,
b,
∵OB=BH+OH,
∴2=![]() b+b,解得b=
b+b,解得b=![]() ,
,
∴M(0,![]() ),N(
),N(,0);
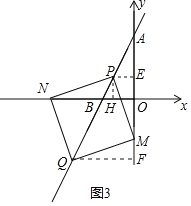
如图3,过点P作PH⊥![]() 轴于H,PE⊥y轴于E,QF⊥y轴于F,
轴于H,PE⊥y轴于E,QF⊥y轴于F,
易得:△PAE~△BAO,
∴![]() ,
,
设PE=c,则AE=2c,
同理证得△PNH△PME,
∴PH=PE=OE=c,则AE=2c,
∵OA=AE+OE,
∴4=2c+c,解得c=![]() ,
,
∵△MQF△PME,
∴MF=PE=OE,EM=FQ,
∴EM=OF=FQ,设EM=OF=FQ=m,
则Q(﹣m,﹣m),代入y=2x+4中,得﹣m=﹣2m+4,解得m=4,
∴NO=NH+OH=![]() ,∴N(
,∴N(![]() ,0),
,0),
∵OF=m=4,
∴M(0,﹣4).
综上所述M(0,![]() ),N(
),N(![]() ,0)或M(0,
,0)或M(0,![]() ),N(
),N(![]() ,0)或M(0,﹣4),N(
,0)或M(0,﹣4),N(![]() ,0).
,0).


科目:初中数学 来源: 题型:
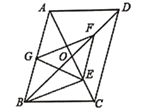
【题目】如图,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:
的中点,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形.
是菱形.
其中正确的是( )
A.①②③B.①③④C.①②⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了准备“欢乐颂——创意市场”,初2020级某同学到批发市场购买了![]() 、
、![]() 两种原材料,
两种原材料,![]() 的单价为每件6元,
的单价为每件6元,![]() 的单价为每件3元.该同学的创意作品需要
的单价为每件3元.该同学的创意作品需要![]() 材料的数量是
材料的数量是![]() 材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
(1)该同学最多购买多少件![]() 材料;
材料;
(2)在该同学购买![]() 材料最多的前提下,用所购买的
材料最多的前提下,用所购买的![]() ,
,![]() 两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高
两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高![]() 标价,但无人问津,于是该同学在标价的基础上降低
标价,但无人问津,于是该同学在标价的基础上降低![]() 出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了
出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
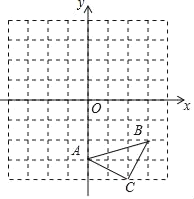
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:直线AB:y=﹣3x+3与两坐标轴交于A,B两点.
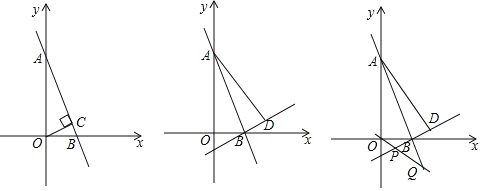
(1)过点O作OC⊥AB于点C,求OC的长;
(2)将△AOB沿AB翻折到△ABD,点O与点D对应,求直线BD的解析式;
(3)在(2)的条件下,正比例函数y=kx与直线BD交于P,直线AB交于Q,若OP=3OQ,求正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形 OABC 的边 OA 与 x 轴重合,B 的坐标为(﹣1,2),将矩形 OABC 绕平面内一点 P 顺时针旋转 90°,使 A、C 两点恰好落在反比例函数 y=![]() 的图象上,则旋转中心 P 点的坐标是( )
的图象上,则旋转中心 P 点的坐标是( )
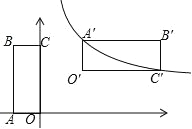
A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
某同学在计算3(4+1)(42+1)时,发现把3写成4-1后,可以连续运用平方差公式计算,
3(4+1)(42+1)
=(4-1)(4+1)(42+1)
=(42-1)(42+1)
=44-1
=256-1
=255.
请借鉴该同学的经验,计算下列各式的值:
(1)(2+1)(22+1)(24+1)(28+1)…(22019+1)
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,正方形ABCD的边长为5,点E、F分别在边AB、AD的延长线上,且BE=DF,连接EF.
(1)证明:EF⊥AC;
(2)将△AEF绕点A顺时针方向旋转,当旋转角α满足0°<α<45°时,设EF与射线AB交于点G,与AC交于点H,如图所示,试判断线段FH、HG、GE的数量关系,并说明理由.
(3)若将△AEF绕点A旋转一周,连接DF、BE,并延长EB交直线DF于点P,连接PC,试说明点P的运动路径并求线段PC的取值范围.
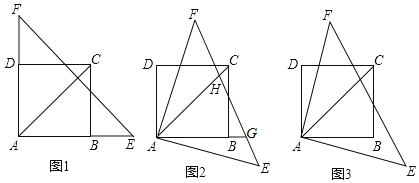
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com