
【题目】如图,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:
的中点,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形.
是菱形.
其中正确的是( )
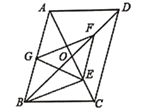
A.①②③B.①③④C.①②⑤D.②③⑤
【答案】B
【解析】
由平行四边形的性质可得OB=BC,由等腰三角形的性质可判断①正确,由直角三角形的性质和三角形中位线定理可判断②错误,通过证四边形BGFE是平行四边形,可判断③正确,由平行线的性质和等腰三角形的性质可判断④正确,由∠BAC≠30°可判断⑤错误.
解:∵四边形ABCD是平行四边形
∴BO=DO=![]() BD,AD=BC,AB=CD,AB∥BC,
BD,AD=BC,AB=CD,AB∥BC,
又∵BD=2AD,
∴OB=BC=OD=DA,且点E是OC中点,
∴BE⊥AC,故①正确,
∵E、F分别是OC、OD的中点,
∴EF∥CD,EF=![]() CD,
CD,
∵点G是Rt△ABE斜边AB上的中点,
∴GE=![]() AB=AG=BG
AB=AG=BG
∴EG=EF=AG=BG,无法证明GE=GF,故②错误,
∵BG=EF,AB∥CD∥EF
∴四边形BGFE是平行四边形,
∴GF=BE,且BG=EF,GE=GE,
∴△BGE≌△FEG(SSS)故③正确
∵EF∥CD∥AB,
∴∠BAC=∠ACD=∠AEF,
∵AG=GE,
∴∠GAE=∠AEG,
∴∠AEG=∠AEF,
∴AE平分∠GEF,故④正确,
若四边形BEFG是菱形
∴BE=BG=![]() AB,
AB,
∴∠BAC=30°
与题意不符合,故⑤错误
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届全国青年运动会将于2019年8月在太原开幕,这是山西历史上第一次举办全国大型综合性运动会,必将推动我市全民健康理念的提高.某体育用品商店近期购进甲、乙两种运动衫各50件,甲种用了2000元,乙种用了2400元.商店将甲种运动衫的销售单价定为60元,乙种运动衫的销售单价定为88元.该店销售一段时间后发现,甲种运动衫的销售不理想,于是将余下的运动衫按照七折销售;而乙种运动衫的销售价格不变.商店售完这两种运动衫至少可获利2460元,求甲种运动衫按原价销售件数的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
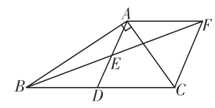
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为![]() cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.

(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是180m2的无盖长方体纸盒,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=2x+4与两坐标轴分别交于A,B两点.
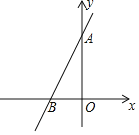
(1)若一次函数y=﹣![]() x+m与直线AB的交点在第二象限,求m的取值范围;
x+m与直线AB的交点在第二象限,求m的取值范围;
(2)若M是y轴上一点,N是x轴上一点,直线AB上是否存在两点P,Q,使得以M,N,P,Q四点为顶点的四边形是正方形.若存在,求出M,N两点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com