
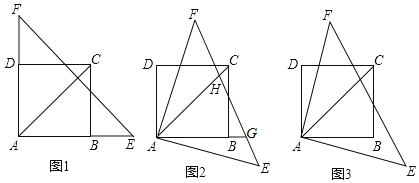
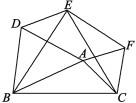
【题目】已知,如图1,正方形ABCD的边长为5,点E、F分别在边AB、AD的延长线上,且BE=DF,连接EF.
(1)证明:EF⊥AC;
(2)将△AEF绕点A顺时针方向旋转,当旋转角α满足0°<α<45°时,设EF与射线AB交于点G,与AC交于点H,如图所示,试判断线段FH、HG、GE的数量关系,并说明理由.
(3)若将△AEF绕点A旋转一周,连接DF、BE,并延长EB交直线DF于点P,连接PC,试说明点P的运动路径并求线段PC的取值范围.
【答案】(1)证明见解析;(2)FH2+GE2=HG2,理由见解析;(3)0≤PC≤5![]() .
.
【解析】
(1)先证明AE=AF,根据等腰三角形三线合一的性质可得结论;
(2)如图2,作辅助线,构建全等三角形,先证明△AGH≌△AGK,得GH=GK,由△AFH≌△AEK,得∠AEK=∠AFH=45°,FH=EK,利用勾股定理得:KG2=EG2+EK2,根据相等关系线段等量代换可得结论:FH2+GE2=HG2;
(3)如图3,先证明∠FPE=∠FAE=90°,根据90°的圆周角所对的弦是直径可得:点P的运动路径是:以BD为直径的圆,如图4,可得PC的取值范围.
(1)证明:如图1,
∵四边形ABCD是正方形,
∴AD=AB,∠DAC=∠BAC,
∵BE=DF,
∴AD+DF=AB+BE,即AF=AE,
∴AC⊥EF;
(2)解:FH2+GE2=HG2,理由是:
如图2,过A作AK⊥AC,截取AK=AH,连接GK、EK,
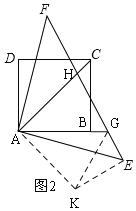
∵∠CAB=45°,
∴∠CAB=∠KAB=45°,
∵AG=AG,
∴△AGH≌△AGK,
∴GH=GK,
由旋转得:∠FAE=90°,AF=AE,
∵∠HAE=90°,
∴∠FAH=∠KAE,
∴△AFH≌△AEK,
∴∠AEK=∠AFH=45°,FH=EK,
∵∠AEH=45°,
∴∠KEG=45°+45°=90°,
Rt△GKE中,KG2=EG2+EK2,
即:FH2+GE2=HG2;
(3)解:如图3,
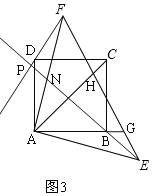
∵AD=AB,∠DAF=∠BAE,AE=AF,
∴△DAF≌△BAE,
∴∠DFA=∠BEA,
∵∠PNF=∠ANE,
∴∠FPE=∠FAE=90°,
∴将△AEF绕点A旋转一周,总存在直线EB与直线DF垂直,
∴点P的运动路径是:以BD为直径的圆,如图4,
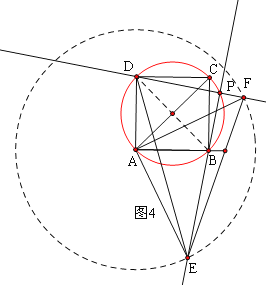
当P与C重合时,PC最小,PC=0,
当P与A重合时,PC最大为5![]() ,
,
∴线段PC的取值范围是:0≤PC≤5![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=2x+4与两坐标轴分别交于A,B两点.
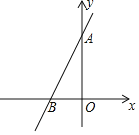
(1)若一次函数y=﹣![]() x+m与直线AB的交点在第二象限,求m的取值范围;
x+m与直线AB的交点在第二象限,求m的取值范围;
(2)若M是y轴上一点,N是x轴上一点,直线AB上是否存在两点P,Q,使得以M,N,P,Q四点为顶点的四边形是正方形.若存在,求出M,N两点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益民商店经销某种商品,进价为每件80元,商店销售该商品每件售价高干8元且不超过120元若售价定为每件120元时,每天可销售200件,市场调查反映:该商品售价在120元的基础上,每降价1元,每天可多销售10件,设该商品的售价为![]() 元,每天销售该商品的数量为
元,每天销售该商品的数量为![]() 件.
件.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)商店在销售该商品时,除成本外每天还需支付其余各种费用1000元,益民商店在某一天销售该商品时共获利8000元,求这一天该商品的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是两根木棒及其影子的情形.
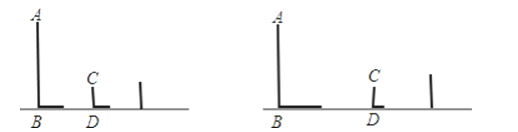
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
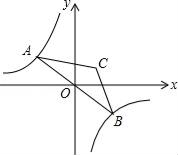
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
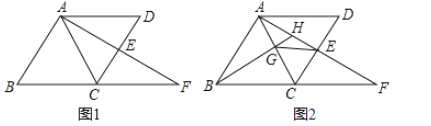
(1)如图1,若![]() ,
,![]() ,求平行四边形
,求平行四边形![]() 的面积;
的面积;
(2)如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,中国工程院院士、“杂交水稻之父”袁隆平团队选育培植的耐盐碱水稻(即海水稻)在山东青岛等六个试验基地开始春播育秧,预计今年的种植规模将超一万亩.已知去年某基地甲、乙两块实验田海水稻的总产量都是3600千克,乙实验田海水稻种植面积是甲实验田的![]() ,而乙实验田海水稻平均亩产量比甲多60千克.
,而乙实验田海水稻平均亩产量比甲多60千克.
(1)求甲、乙两块实验田种植海水稻的面积;
(2)经过科学家的努力,海水稻正从试验田走向餐桌,某电商新购进A、B两种包装的海水稻产品共50袋,其进价、标价及优惠方案如下表所示.若要保证这批海水稻产品全部售出后所得利润不少于1000元,该电商至少要购进A种包装的海水稻产品多少袋?
包装类型 | A | B |
进价(元/袋) | 100 | 30 |
标价(元/袋) | 150 | 50 |
优惠方案 | 全部九折 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,点A在BC边的上方,把△ABC绕点B逆时针方向旋转60°得△DBE,绕点C顺时针方向旋转60°得△FEC,连接AD,AF.
(1)△ABD,△ACF,△BCE是什么特殊三角形?请说明理由;
(2)当△ABC满足什么条件时,四边形ADEF是正方形?请说明理由;
(3)当△ABC满足什么条件时,以点A,D,E,F为顶点的四边形不存在?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com