
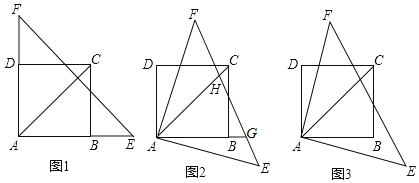
【题目】如图,平行四边形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
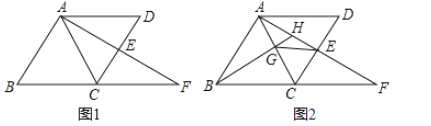
(1)如图1,若![]() ,
,![]() ,求平行四边形
,求平行四边形![]() 的面积;
的面积;
(2)如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)首先证明CE⊥AF,想办法求出CD,AE即可解决问题. (2)证明:如图2中,连接BE,作EK⊥AC于K.利用全等三角形的性质证明AG=EK=KG,即可解决问题.
(1)解:如图1中,
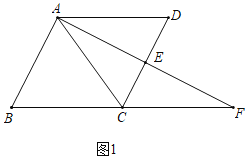
∵CA=CF,AE=EF, ∴CE⊥AF, ∵CE=1,∠F=30°,
∴CF=CA=2CE=2,AE=EF=![]() ,
,
∵四边形ABCD 平行四边形, ∴AD∥CF, ∴∠D=∠ECF,
∵∠AED=∠CEF,AE=EF, ∴△ADE≌△FCE(AAS),
∴CE=DE=1, ∴CD=2,
∴平行四边形ABCD的面积=CDAE=![]() .
.
(2)证明:如图2中,连接BE,作EK⊥AC于K.
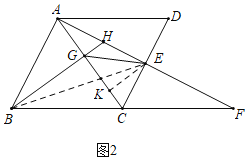
∵CE⊥AF,CE∥AB, ∴AB⊥AE,
∵BG⊥AC, ∴∠BAH=∠AEC=∠AGB=90°,
∴∠ABG+∠BAG=90°,∠BAG+∠CAE=90°,
∴∠ABH=∠CAE, ∵BH=AC, ∴△BAH≌△AEC(AAS),
∴BA=AE=CD,AH=CE=DE, ∴AB=2AH,
∵∠ABG=∠EAK,AB=AE,∠AGB=∠AKE,
∴△BGA≌△AKE(AAS), ∴AG=EK,
∴tan∠ABH=![]() =
=![]() =
=![]() ,
,
∴tan∠EAK=![]() =
=![]() , ∴AK=2EK, ∴AG=GK, ∴KG=KE,
, ∴AK=2EK, ∴AG=GK, ∴KG=KE,
∵∠EKG=90°, ∴EG=![]() =
=![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,如图:直线AB:y=﹣3x+3与两坐标轴交于A,B两点.
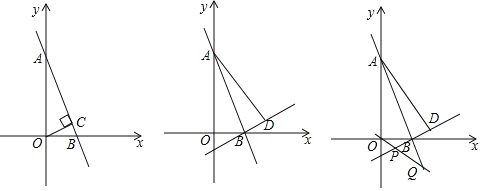
(1)过点O作OC⊥AB于点C,求OC的长;
(2)将△AOB沿AB翻折到△ABD,点O与点D对应,求直线BD的解析式;
(3)在(2)的条件下,正比例函数y=kx与直线BD交于P,直线AB交于Q,若OP=3OQ,求正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,正方形ABCD的边长为5,点E、F分别在边AB、AD的延长线上,且BE=DF,连接EF.
(1)证明:EF⊥AC;
(2)将△AEF绕点A顺时针方向旋转,当旋转角α满足0°<α<45°时,设EF与射线AB交于点G,与AC交于点H,如图所示,试判断线段FH、HG、GE的数量关系,并说明理由.
(3)若将△AEF绕点A旋转一周,连接DF、BE,并延长EB交直线DF于点P,连接PC,试说明点P的运动路径并求线段PC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.

(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
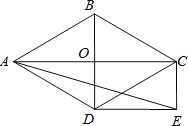
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com