
【题目】阅读以下材料,并按要求完成相应的任务.
已知平面上两点![]() ,则所有符合
,则所有符合![]() 且
且![]() 的点
的点![]() 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
(问题)如图1,在平面直角坐标中,在![]() 轴,
轴,![]() 轴上分别有点
轴上分别有点![]() ,点
,点![]() 是平面内一动点,且
是平面内一动点,且![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.

阿氏圆的关键解题步骤:
第一步:如图1,在![]() 上取点
上取点![]() ,使得
,使得![]() ;
;
第二步:证明![]() ;第三步:连接
;第三步:连接![]() ,此时
,此时![]() 即为所求的最小值.
即为所求的最小值.
下面是该题的解答过程(部分):
解:在![]() 上取点
上取点![]() ,使得
,使得![]() ,
,
又![]() .
.
任务:
![]() 将以上解答过程补充完整.
将以上解答过程补充完整.
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为
为![]() 内一动点,满足
内一动点,满足![]() ,利用
,利用![]() 中的结论,请直接写出
中的结论,请直接写出![]() 的最小值.
的最小值.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的表达式是![]() ,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=
,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=![]() 时,m的值为( )
时,m的值为( )
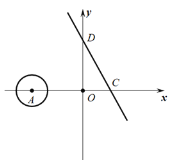
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某校举行冬季运动会,其中一个项目是乒乓球比赛,比赛为单循环制,即所有参赛选手彼此恰好比赛一场. 记分规则是:每场比赛胜者得3分、负者得0分、平局各得1分. 赛后统计,所有参赛者的得分总知为210分,且平局数不超过比赛总场数的![]() ,本次友谊赛共有参赛选手__________人.
,本次友谊赛共有参赛选手__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.
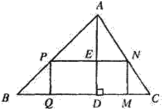
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点 M 满足横、纵坐标都为整数,则把点 M 叫做“整点”.例如:P(1,0)、Q(2,-2)都是“整点”.抛物线 y=mx2-2mx+m-1(m>0)与 x 轴交于 A、 B 两点,若该抛物线在 A、B 之间的部分与线段 AB 所围成的区域(包括边界)恰有 6 个整点,则 m 的取值范围是( )
A.![]() m
m ![]() B.
B.![]() m
m ![]() C.
C.![]() m
m ![]() D.
D.![]() m
m ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
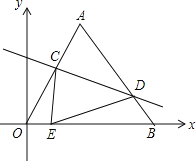
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,0),经过A点的直线交抛物线于点D (2, 3).
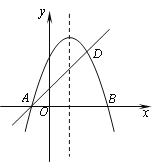
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点E (a,0) 作直线EF∥AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
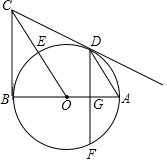
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
(1)求证:点E是弧BD的中点;
(2)求证:CD是⊙O的切线;
(3)若tan∠ADG=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com