
【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移 ![]() 个单位长度得到三角形
个单位长度得到三角形 ![]() ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为 ![]() ,
,![]() ,
,![]() .
.
(1)写出点 ![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)在图中画出平移后的三角形 ![]() ;
;
(3)三角形 ![]() 的面积为__________.
的面积为__________.

科目:初中数学 来源: 题型:
【题目】学完二次根式一章后,小易同学看到这样一题:“函数![]() 中,自变量
中,自变量![]() 的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量
的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量![]() 的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
第一步:函数![]() 中,自变量
中,自变量![]() 的取值范围是_____________.
的取值范围是_____________.
第二步:根据自变量取值范围列表:
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
![]() __________.
__________.
第三步:描点画出函数图象.
在描点的时候,遇到了![]() ,
,![]() 这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:

你能否从中得到启发,在下面的![]() 轴上标出表示
轴上标出表示![]() 、
、![]() 、
、![]() 的点,并画出
的点,并画出![]() 的函数图象.
的函数图象.

第四步:分析函数的性质.
请写出你发现的函数的性质(至少写两条):
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步:利用函数![]() 图象解含二次根式的方程和不等式.
图象解含二次根式的方程和不等式.
(1)请在上面坐标系中画出![]() 的图象,并估算方程
的图象,并估算方程![]() 的解.
的解.
(2)不等式![]() 的解是__________________.
的解是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
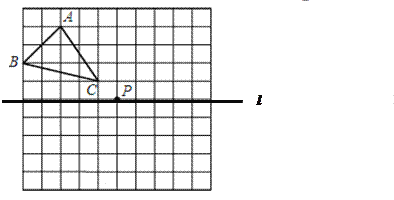
【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
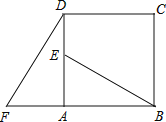
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F,AB=6cm,AD=8cm.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.判断四边形FBGD的形状,并说明理由.
(3)在(2)的条件下,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
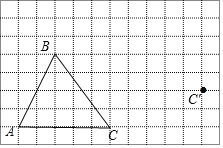
(1)画出平移后的△A′B′C′.
(2)画出AB边上的中线线CD;
(3)在整个平移过程中,线段BC扫过的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,如图∠BAC=90°,BD平分∠ABC,点E在BC上,DE∥AB,点F在BC上,连结AF,∠C=36°.
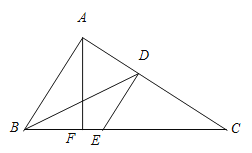
(1)求∠BDE的度数;
(2)若∠BAF∶∠CAF=2∶3,求证:AF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
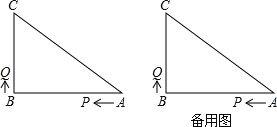
【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com