练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
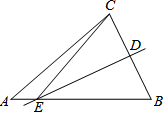
    5．如图，在△ABC中，直线ED是线段BC的垂直平分线，直线ED分别交BC、AB于点D、点E，已知BD=4，△ABC的周长为20，则△AEC的周长为（　　）
    A．24B．20C．16D．12

    分析 由BC的垂直平分线交AB于点E，可得BE=CE，又由△ABC的周长为10，BC=4，易求得△ACE的周长是△ABC的周长-BC，继而求得答案．

    解答 解：∵BC的垂直平分线交AB于点E，
    ∴BE=CE，
    ∵△ABC的周长为20，BC=2BD=8，
    ∴△ACE的周长是：AE+CE+AC=AE+BE+AC=AB+AC=AB+AC+BC-BC=20-8=12．
    故选D．

    点评 此题考查了线段垂直平分线的性质．此题难度不大，注意数形结合思想与整体思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．若关于x的一元二次方程x2+（3a-1）x+a+12=0有两个不相等的实根x1，x2，且x1≤0、x2＞1，则实数a的取值范围是-12≤a＜-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=$\frac{1}{2}$∠ABC．以点B为旋转中心，将△BEC按逆时针方向旋转至△BEA（点C与点A重合，点E到点E处），连接DE．求证：DE'=DE．
    （2）如图2，在△ABC中，BA=BC，∠ABC=90°，点D，E是AC边上的两点，且∠DBE=45°（即∠DBE=$\frac{1}{2}$∠ABC）．求证：DE2=AD2+EC2．
    （3）如图3，在△ABC中，BA=BC，∠ABC=90°，点E是AC边上的点，点D是CA边延长线上的点，且∠DBE=45°．第（2）题中的结论：DE2=AD2+EC2还成立吗？如果成立，请给出证明；如果不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知线段a，b，其中a＞b，求作直角三角形ABC，使得∠C为直角，AB=a，AC=b（尺规作图，保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．先化简，再求值：$\frac{x-3}{x-2}$÷（x+2-$\frac{5}{x-2}}$），其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

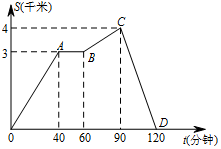    10．为了提高身体素质，小明假期为自己制定了慢跑锻炼计划，某日小明从省体育场出发沿长安路慢跑，已知他离省体育场的距离s（ km）与时间t（h）之间的关系如图所示，根据图象回答下列问题：
    （1）小明离开省体育场的最远距离是4千米，他在120分钟内共跑了8千米；
    （2）小明在这次慢跑过程中，停留所用的时间为20分钟；
    （3）小明在这段时间内慢跑的最快速度是每小时8千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列计算正确的是（　　）
    A．3a+2b=5abB．（2a）3=6a3C．a3•a2=a5D．（x-2）2=x2-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．一个多边形的每一个内角均为相邻外角的4倍，这个多边形的边数是（　　）
    A．9B．10C．11D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）（3-$\sqrt{7}$）（3+$\sqrt{7}$）+$\sqrt{2}$（2-$\sqrt{2}$）
    （2）4cos30°-|$\sqrt{3}$-2|+${（\frac{\sqrt{5}-1}{2}）}^{0}$-$\sqrt{27}$+${（-\frac{1}{3}）}^{-2}$．

    查看答案和解析>>

    同步练习册答案