
分析 将一元二次方程的解转化为抛物线与x轴的交点问题,画出函数图象结合题意即可得出关于a的一元一次不等式组,解之即可得出结论.
解答 解:令y=x2+(3a-1)x+a+12,则(x1,0)、(x2,0)为抛物线与x轴的交点坐标,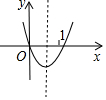
依此画出函数图象,如图所示.
根据题意得:$\left\{\begin{array}{l}{a+12≥0}\\{1+3a-1+a+12<0}\\{-\frac{3a-1}{2}>\frac{1}{2}}\end{array}\right.$,
解得:-12≤a<-3.
故答案为:-12≤a<-3.
点评 本题考查了抛物线与x轴的交点、二次函数的图象以及解一元一次不等式组,将一元二次方程的解转化为抛物线与x轴的交点是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | 0既不是正数,也不是负数 | |
| B. | 最小的有理数是0 | |
| C. | 绝对值最小的有理数是0 | |
| D. | 除以一个不为0的数等于乘以这个数的倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.| 四边形ABCD | 菱形 | 矩形 | 平行四边形 |
| 四边形EFGH | 矩形 | 菱形 | 平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{y}{3{x}^{2}}}$=$\frac{1}{3x}$$\sqrt{y}$ | B. | $\sqrt{{x}^{2}+{y}^{2}}$=x+y | C. | $\sqrt{\frac{3x}{8{y}^{3}}}$=$\frac{1}{4{y}^{2}}$$\sqrt{6xy}$ | D. | 3$\sqrt{\frac{2y}{3}}$=$\sqrt{2y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
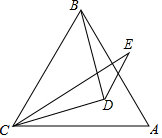 如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.
如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
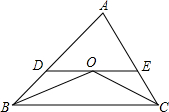 如图,△ABC中,AB=5,AC=4,BO,CO分别平分∠ABC,∠ACB,过点O作直线平行于BC,交AB、AC于D、E,则△ADE的周长为( )
如图,△ABC中,AB=5,AC=4,BO,CO分别平分∠ABC,∠ACB,过点O作直线平行于BC,交AB、AC于D、E,则△ADE的周长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
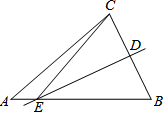 如图,在△ABC中,直线ED是线段BC的垂直平分线,直线ED分别交BC、AB于点D、点E,已知BD=4,△ABC的周长为20,则△AEC的周长为( )
如图,在△ABC中,直线ED是线段BC的垂直平分线,直线ED分别交BC、AB于点D、点E,已知BD=4,△ABC的周长为20,则△AEC的周长为( )| A. | 24 | B. | 20 | C. | 16 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com