
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.
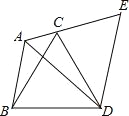
【答案】∠BAD=60°,AD=8.
【解析】
根据旋转的性质先证明△ADE是等边三角形,由相似三角形的性质可得∠EAD=60°,AD=AE,即可得到∠BAD=∠BAC﹣∠CAD=60°,AD=AE=AC+CE=AC+AB=3+5=8.
∵△ABD≌△ECD,
∴AD=DE,∠BDA=∠DCE,
∴∠BDC=∠ADE=60°,∠ABD=∠ECD,
∵∠BAC=120°,∠BDC=60°,
∴∠BAC+∠BDC=180°,
∴∠ABD+∠ACD=180°,
∴∠ACD+∠ECD=180°,
∴A、C、E共线,
∴△ADE是等边三角形,
∴∠EAD=60°,AD=AE,
∴∠BAD=∠BAC﹣∠CAD=60°,
∴AD=AE=AC+CE=AC+AB=3+5=8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,经过A、B的直线
,经过A、B的直线![]() 以每秒1个单位的
以每秒1个单位的
速度向下作匀速平移运动,与此同时,点P从点B出发,在直线![]() 上以每秒1个单位的速度沿直线
上以每秒1个单位的速度沿直线![]() 向右下方向作匀速运动.设它们运动的时间为
向右下方向作匀速运动.设它们运动的时间为![]() 秒.
秒.

(1)用含![]() 的代数式表示点P的坐标;
的代数式表示点P的坐标;
(2)过O作OC⊥AB于C,过C作CD⊥![]() 轴于D,问:
轴于D,问: ![]() 为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时
为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时![]() 与直线CD的位置关系.
与直线CD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
【1】请用画树形图或列表的方法求小敏去看比赛的概率;
【2】哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
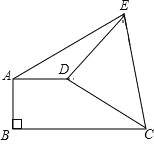
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下内容,再解决问题.
在把多项式m2﹣4mn﹣12n2进行因式分解时,虽然它不符合完全平方公式,但是经过变形,可以利用完全平方公式进行分解:
m2﹣4mn﹣12n2=m2﹣4mn+4n2﹣4n2﹣12n2=(m﹣2n)2﹣16n2=(m﹣6n)(m+2n),像这样构造完全平方式的方法我们称之为“配方法”,利用这种方法解决下面问题.
(1)把多项式因式分解:a2﹣6ab+5b2;
(2)已知a、b、c为△ABC的三条边长,且满足4a2﹣4ab+2b2+3c2﹣4b﹣12c+16=0,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一黄金周期间,海洋中学决定组织部分优秀老师去北京旅游,天马旅行社推出如下收费标准:

(1)学校规定,人均旅游费高于700元,但又想低于1000元,那么该校所派人数应在什么范围内;
(2)已知学校已付旅游费27000元,问该校安排了多少名老师去北京旅游?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com