
【题目】(阅读)如图①,![]() 是等边三角形,将直角三角板
是等边三角形,将直角三角板![]() 的
的![]() 角顶点
角顶点![]() 放在边
放在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),使两边分别交边
重合),使两边分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .进而可证:
.进而可证:![]() .
.
小明的做法是,先证![]() ,再证
,再证![]() ,可证得
,可证得![]() ∽
∽![]() .
.
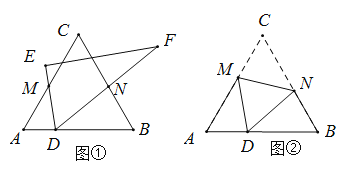
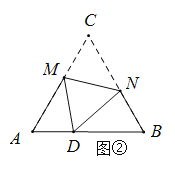
(探究)如图②,将等边三角形![]() 沿折痕
沿折痕![]() 折叠,使点
折叠,使点![]() 的对称点
的对称点![]() 落在边
落在边![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),求证:
重合),求证:![]() ∽
∽![]() .
.
(应用)若图②中的![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】【探究】证明见解析;【应用】![]() .
.
【解析】
【探究】
由折叠的性质可知∠MDN=∠C=60°,然后根据平角的定义和三角形的内角和定理可得∠AMD=∠BDN,再根据等边三角形的性质和相似三角形的判定方法即可证得结论;
【应用】
设CM=MD=x,CN=DN=y,则有AM=3-x,BN=3-y,然后利用相似三角形的性质可得关于x、y的方程组,解方程组即可求出x、y的值,问题即得解决.
解:【探究】∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵将等边△![]() 沿折痕
沿折痕![]() 折叠,点
折叠,点![]() 的对称点
的对称点![]() 落在边
落在边![]() 上,
上,
∴∠MDN=∠C=60°,
∴∠ADM+∠BDN=120°,
∵∠ADM+∠AMD=180°-∠A=180°-60°=120°,
∴∠AMD=∠BDN,
∴![]() ∽
∽![]() ;
;
【应用】∵将等边△![]() 沿折痕
沿折痕![]() 折叠,点
折叠,点![]() 的对称点
的对称点![]() 落在边
落在边![]() 上,
上,
∴CM=MD,CN=DN,
设CM=MD=x,CN=DN=y,
∵AB=AC=BC=3,AD=1,
∴AM=3-x,BN=3-y,BD=2,
∵![]() ∽
∽![]() ,
,
∴![]() ,
,
即![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
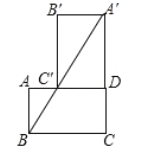
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 分别落在点
分别落在点![]() ,
,![]() ,
,![]() 处.
处.
(1)直接填空:当![]() 时,点
时,点![]() 所经过的路径的长为___________;
所经过的路径的长为___________;
(2)若点![]() ,
,![]() ,
,![]() 在同一直线上,求
在同一直线上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径在矩形
为直径在矩形![]() 内作半圆
内作半圆![]() .
.
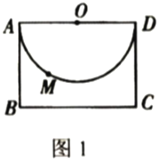
(1)若点![]() 是半圆
是半圆![]() 上一点,则点
上一点,则点![]() 到
到![]() 的最小距离为________;
的最小距离为________;
(2)如图2,保持矩形![]() 固定不动,将半圆
固定不动,将半圆![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]()
![]() 度,得到半圆
度,得到半圆![]() ,则当半圆
,则当半圆![]() 与
与![]() 相切时,求旋转角
相切时,求旋转角![]() 的度数;
的度数;

(3)在旋转过程中,当![]() 与边
与边![]() 有交点时,求
有交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
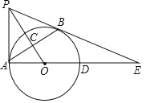
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
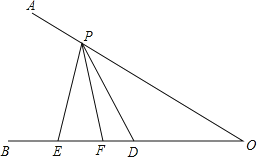
【题目】如图,已知∠AOB=30°,点P在边OA上,OP=14,点E,F在边OB上,PE=PF,EF=6.若点D是边OB上一动点,则∠PDE=45°时,DF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com