
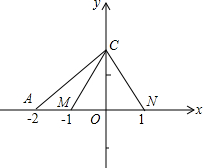
 如图,在直角坐标系中,△CMN是等边三角形,且OM=ON=1,OA=2,P是x轴正半轴上的任意一点,当P点在x轴正半轴上移动时,是否存在这样的一点P,使△CMA∽△CNP?若存在,请确定P点的位置并画出△CNP,并给予证明;若不存在,请说明理由.
如图,在直角坐标系中,△CMN是等边三角形,且OM=ON=1,OA=2,P是x轴正半轴上的任意一点,当P点在x轴正半轴上移动时,是否存在这样的一点P,使△CMA∽△CNP?若存在,请确定P点的位置并画出△CNP,并给予证明;若不存在,请说明理由.| CM |
| CN |
| MA |
| NP |
| 2 |
| 2 |
| 1 |
| NP |
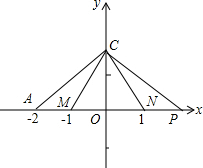
| CM |
| CN |
| MA |
| NP |
| 2 |
| 2 |
| 1 |
| NP |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
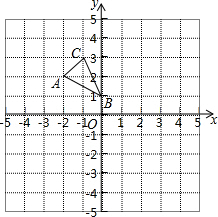 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:
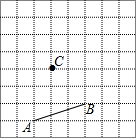 在如图所示的方格纸中,每一个正方形的面积为1,按要求画图,并回答问题.
在如图所示的方格纸中,每一个正方形的面积为1,按要求画图,并回答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com