
分析 分两种情况:(1)如图1,点C在第一象限,(2)如图2,点C在第四象限.针对每一种情况,分别画出图形,再利用全等求出距离,从而得出C点坐标.
解答 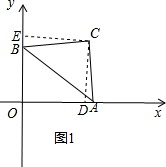 解:分两种情况:
解:分两种情况:
(1)如图1,过点C作CD⊥OA于D,CE⊥OB于E.
∵∠BCA=∠DCE=90°,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD,CE=CD=OE,
∵AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BC=$\frac{\sqrt{2}}{2}$AB=$\frac{5\sqrt{2}}{2}$,
CE2+(CE-3)2=BC2=$\frac{25}{2}$,
解得CE=$\frac{7}{2}$或-$\frac{1}{2}$(不合题意舍去).
则点C坐标为($\frac{7}{2}$,$\frac{7}{2}$);
(2)如图2,过点C作CD⊥OA于D,CE⊥OB于E.
∵∠BCA=∠DCE=90°,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠BCE}\\{AC=BC}\\{\;}\end{array}\right.$,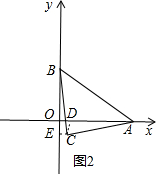
∴△ACD≌△BCE,
∴BE=AD,CE=CD=OE,
∵AB=5,
∴BC=$\frac{5\sqrt{2}}{2}$,
CE2+(CE+6)2=BC2=$\frac{25}{2}$,
解得CE=$\frac{1}{2}$或-$\frac{7}{2}$(不合题意舍去).
则点C坐标为($\frac{1}{2}$,-$\frac{1}{2}$).
综上可知点C坐标为($\frac{1}{2}$,-$\frac{1}{2}$)和($\frac{7}{2}$,$\frac{7}{2}$).
点评 本题考查了坐标与图形性质,等腰直角三角形的性质,作出辅助线构建全等三角形是本题的关键,并注意分类思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在证明含30°角的直角三角形的性质时,有的同学采用了下面的做法:
在证明含30°角的直角三角形的性质时,有的同学采用了下面的做法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
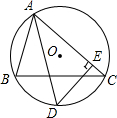 如图,⊙O为△ABC的外接圆,$\widehat{BD}$=$\widehat{CD}$,DE⊥AC于E,AB=4,AC=6,求CE的长.
如图,⊙O为△ABC的外接圆,$\widehat{BD}$=$\widehat{CD}$,DE⊥AC于E,AB=4,AC=6,求CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com