
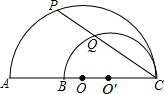
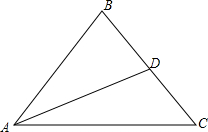
 如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )| A. | 10cm | B. | 10$\sqrt{3}$cm | C. | 12cm | D. | 16cm |
分析 连接BQ,AP,如图,由于AC,BC为直径,根据圆周角定理得∠APC=90°,∠BQC=90°,再根据含30度的直角三角形三边的关系得到PC=$\frac{\sqrt{3}}{2}$AC,CQ=$\frac{\sqrt{3}}{2}$BC,PQ=PC-CQ=$\frac{\sqrt{3}}{2}$(AC-BC)=$\frac{\sqrt{3}}{2}$AB=10$\sqrt{3}$.
解答 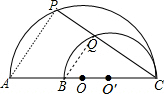 解:连接BQ,AP,如图,
解:连接BQ,AP,如图,
∵AC,BC为直径,
∴∠APC=90°,∠BQC=90°,
∵∠ACP=30°,
∴PC=$\frac{\sqrt{3}}{2}$AC,CQ=$\frac{\sqrt{3}}{2}$BC,
∴PQ=PC-CQ=$\frac{\sqrt{3}}{2}$(AC-BC)=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×20=10$\sqrt{3}$(cm).
故选B.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质以及直径所对的圆周角为直角.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 12 | C. | 10或12 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
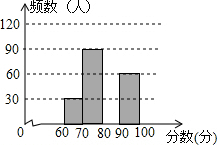 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
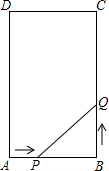 如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题:
如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值.
(1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com