
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯ![]() Ј¬ѕ№эµг
Ј¬ѕ№эµг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ИэµгЈ®
ИэµгЈ®
![]() ЗуЕЧОпПЯµДЅвОцКЅј°¶ҐµгMµДЧш±кЈ»
ЗуЕЧОпПЯµДЅвОцКЅј°¶ҐµгMµДЧш±кЈ»
![]() Б¬ЅУACЎўMBЈ¬PОЄПЯ¶ОMBЙПµДТ»ёц¶ЇµгЈЁІ»УлµгMЎўBЦШєПЈ©Ј¬№эµгPЧчxЦбµДґ№ПЯPQЈ¬ИфOQ=aЈ¬ЛД±ЯРОACPQµДГж»эОЄsЈ¬ЗуaОЄєОЦµК±Ј¬Гж»эsЧоґуЈ»
Б¬ЅУACЎўMBЈ¬PОЄПЯ¶ОMBЙПµДТ»ёц¶ЇµгЈЁІ»УлµгMЎўBЦШєПЈ©Ј¬№эµгPЧчxЦбµДґ№ПЯPQЈ¬ИфOQ=aЈ¬ЛД±ЯРОACPQµДГж»эОЄsЈ¬ЗуaОЄєОЦµК±Ј¬Гж»эsЧоґуЈ»
![]() µгNКЗЕЧОпПЯЙПµЪЛДПуПЮµДТ»ёц¶ЁµгЈ¬Чш±кОЄ
µгNКЗЕЧОпПЯЙПµЪЛДПуПЮµДТ»ёц¶ЁµгЈ¬Чш±кОЄ![]() Ј¬№эµгCЧчЦ±ПЯ
Ј¬№эµгCЧчЦ±ПЯ![]() ЦбЈ¬¶Їµг
ЦбЈ¬¶Їµг![]() ФЪЦ±ПЯlЙПЈ¬¶Їµг
ФЪЦ±ПЯlЙПЈ¬¶Їµг![]() ФЪxЦбЙПЈ¬Б¬ЅУPMЎўPQЎўNQЈ¬µ±mОЄєОЦµК±Ј¬
ФЪxЦбЙПЈ¬Б¬ЅУPMЎўPQЎўNQЈ¬µ±mОЄєОЦµК±Ј¬![]() µДєНЧоРЎЈ¬ІўЗуіц
µДєНЧоРЎЈ¬ІўЗуіц![]() єНµДЧоРЎЦµЈ®
єНµДЧоРЎЦµЈ®

Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»MЈЁ1,4Ј©
Ј»MЈЁ1,4Ј©
ЈЁ2Ј©µ±![]() Ј¬
Ј¬![]() Гж»эЧоґуЈ¬ЧоґуОЄ
Гж»эЧоґуЈ¬ЧоґуОЄ![]() .
.
ЈЁЈіЈ©![]()
ЎѕЅвОцЎї
ЈЁ1Ј©ЕЧОпПЯ![]() №э
№э![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() їЙЗуµГЅвОцКЅЈ»
їЙЗуµГЅвОцКЅЈ»
ЈЁ2Ј©Ѕ«![]() УГє¬
УГє¬![]() µДґъКэКЅ±нКѕЈ¬ІўЕд·ЅіЙ¶ҐµгКЅЗуіцЧоґуЦµЈ»
µДґъКэКЅ±нКѕЈ¬ІўЕд·ЅіЙ¶ҐµгКЅЗуіцЧоґуЦµЈ»
ЈЁ3Ј©ёщѕЭСЎЦ·ФмЗЕДЈРНЈ¬Ѕ«¶Ґµг![]() ПтПВЖЅТЖИэёцµҐО»µГ
ПтПВЖЅТЖИэёцµҐО»µГ![]() Ј¬µ±
Ј¬µ±![]() ФЪН¬Т»МхЦ±ПЯЙПК±Ј¬
ФЪН¬Т»МхЦ±ПЯЙПК±Ј¬![]() ИЎµГЧоРЎЦµ.
ИЎµГЧоРЎЦµ.
(1)ЎЯЕЧОпПЯ![]() ѕ№эµг
ѕ№эµг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ,
,
Ўа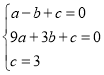 ЅвµГ
ЅвµГ
Ўа![]() =
=![]() ,¶ҐµгMµДЧш±кОЄЈЁ1,4Ј©
,¶ҐµгMµДЧш±кОЄЈЁ1,4Ј©
ЈЁ2Ј©Б¬ЅУACЎўMBЈ¬PОЄПЯ¶ОMBЙПµДТ»ёц¶ЇµгЈЁІ»УлµгMЎўBЦШєПЈ©Ј¬№эµгPЧчxЦбµДґ№ПЯPQ.ЙиPµгµДЧш±кОЄ![]() Ј¬ИзНјЛщКѕ.
Ј¬ИзНјЛщКѕ.

ЎЯPФЪЦ±ПЯMBЙПЈ¬![]() Ј¬
Ј¬![]() Ј¬ЙиЦ±ПЯMBОЄ
Ј¬ЙиЦ±ПЯMBОЄ![]()
![]() ЅвµГ
ЅвµГ![]()
Ц±ПЯMBµДЅвОцКЅОЄ![]() Ј¬PµгЧш±кОЄ
Ј¬PµгЧш±кОЄ![]()
ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]()
Ўа![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
ЎЯ![]()
ХыАн![]()
Ўајґµ±![]() Ј¬
Ј¬![]() Гж»эЧоґуЈ¬ЧоґуОЄ
Гж»эЧоґуЈ¬ЧоґуОЄ![]() .
.
ЈЁ3Ј©Ѕ«¶Ґµг![]() ПтПВЖЅТЖИэёцµҐО»µГ
ПтПВЖЅТЖИэёцµҐО»µГ![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ѕ»
Ѕ»![]() ЦбУЪµг
ЦбУЪµг![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј®ИзНјЛщКѕЈ¬Фт
Ј®ИзНјЛщКѕЈ¬Фт![]() .
.
ЎЯ![]() Ј¬
Ј¬![]()
Ўа![]() ЦбЈ¬ЗТ
ЦбЈ¬ЗТ![]()
Ўа![]() Ј¬ЛД±ЯРО
Ј¬ЛД±ЯРО![]() ОЄЖЅРРЛД±ЯРО
ОЄЖЅРРЛД±ЯРО
Ўа![]() ,УРНјЦЄ
,УРНјЦЄ![]() Иэµг№ІПЯК±Ј¬
Иэµг№ІПЯК±Ј¬![]() ИЎЧоРЎЦµ.
ИЎЧоРЎЦµ.
ЙиЦ±ПЯ![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬Ѕ«µг
Ј¬Ѕ«µг![]() Ј¬N
Ј¬N![]()
ЗуµГЦ±ПЯ![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬
Ј¬
µ±![]() К±Ј¬
К±Ј¬![]() Ј¬јґ
Ј¬јґ![]() Ј¬јґ
Ј¬јґ![]() Ј¬
Ј¬
ґЛК±№эµг![]() Чч
Чч![]() ЦбЅ»
ЦбЅ»![]() СУі¤ПЯУлµг
СУі¤ПЯУлµг![]() Ј¬
Ј¬
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() ,
,
Ўа![]() ,јґ
,јґ![]() ,
,
Ўаµ±![]() К±Ј¬
К±Ј¬![]() µДЧоРЎЦµОЄ
µДЧоРЎЦµОЄ![]() .
.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
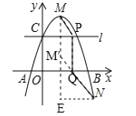
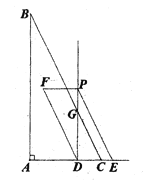
ЎѕМвДїЎїИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПCЈЅ90ЎгЈ¬ТФBCОЄЦ±ѕ¶µДЎСOЅ»ABУЪEЈ¬ODЎНBCЅ»ЎСOУЪDЈ¬DEЅ»BCУЪFЈ¬µгPОЄCBСУі¤ПЯЙПµДТ»µгЈ¬СУі¤PEЅ»ACУЪGЈ¬PEЈЅPF
ЈЁ1Ј©ЗуЦ¤ЈєЦ±ПЯPGОЄЎСOµДЗРПЯЈ»
ЈЁ2Ј©ЗуЦ¤ЈєGAЈЅGEЈ»
ЈЁ3Ј©ЕР¶ПOGУлBEµДО»ЦГ№ШПµЈ¬ІўЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
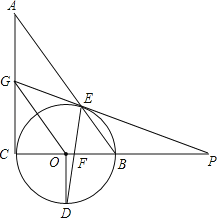
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ТСЦЄЎчABCµДИэёц¶ҐµгЧш±к·Ц±рКЗAЈЁ1Ј¬1Ј©Ј¬BЈЁ4Ј¬1Ј©Ј¬CЈЁ3Ј¬3Ј©Ј®
ЈЁ1Ј©Ѕ«ЎчABCПтПВЖЅТЖ5ёцµҐО»єуµГµЅЎчA1B1C1Ј¬Зл»іцЎчA1B1C1Ј»
ЈЁ2Ј©Ѕ«ЎчABCИЖФµгOДжК±ХлРэЧЄ90ЎгєуµГµЅЎчA2B2C2Ј¬Зл»іцЎчA2B2C2Ј»
ЈЁ3Ј©ЕР¶ПТФOЈ¬A1Ј¬BОЄ¶ҐµгµДИэЅЗРОµДРОЧґЈ®ЈЁОЮРлЛµГчАнУЙЈ©

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
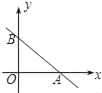
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Т»ґОєЇКэµДНјПуУлЧш±кЦбО§іЙµДИэЅЗРОЈ¬ЅРЧцґЛТ»ґОєЇКэµДЧш±кИэЅЗРОЈ®АэИзЈ¬НјЦРµДТ»ґОєЇКэµДНјПуУлxЈ¬yЦб·Ц±рЅ»УЪµгAЈ¬BЈ¬ФтЎчOABОЄґЛєЇКэµДЧш±кИэЅЗРОЈ®
ЈЁ1Ј©ЗуєЇКэy=![]() x+3µДЧш±кИэЅЗРОµДИэМх±Яі¤Ј»
x+3µДЧш±кИэЅЗРОµДИэМх±Яі¤Ј»
ЈЁ2Ј©ИфєЇКэy=![]() x+bЈЁbОЄіЈКэЈ©µДЧш±кИэЅЗРОЦЬі¤ОЄ16Ј¬ЗуґЛИэЅЗРОГж»эЈ®
x+bЈЁbОЄіЈКэЈ©µДЧш±кИэЅЗРОЦЬі¤ОЄ16Ј¬ЗуґЛИэЅЗРОГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬µг
Ј¬µг![]() ФЪ±Я
ФЪ±Я![]() ЙПЈ¬
ЙПЈ¬![]() Ј¬ЙдПЯ
Ј¬ЙдПЯ![]() Ѕ»
Ѕ»![]() УЪµг
УЪµг![]() Ј¬µг
Ј¬µг![]() ґУµг
ґУµг![]() іц·ўЈ¬ТФГїГл
іц·ўЈ¬ТФГїГл![]() ёцµҐО»і¤¶ИµДЛЩ¶ИСШЙдПЯ
ёцµҐО»і¤¶ИµДЛЩ¶ИСШЙдПЯ![]() ·ЅПтФЛ¶ЇЈ¬№эµг
·ЅПтФЛ¶ЇЈ¬№эµг![]() Чч
Чч![]() Ј¬Ѕ»ЙдПЯ
Ј¬Ѕ»ЙдПЯ![]() УЪµг
УЪµг![]() Ј¬ТФ
Ј¬ТФ![]() Ўў
Ўў![]() ОЄБЪ±ЯЧч
ОЄБЪ±ЯЧч![]() Ј¬Йиµг
Ј¬Йиµг![]() µДФЛ¶ЇК±јдОЄ
µДФЛ¶ЇК±јдОЄ![]() .
.
ЈЁ1Ј©ПЯ¶О![]() µДі¤ОЄ ЈЁУГє¬
µДі¤ОЄ ЈЁУГє¬![]() µДґъКэКЅ±нКѕЈ©
µДґъКэКЅ±нКѕЈ©
ЈЁ2Ј©Зуµг![]() ВдФЪ
ВдФЪ![]() ЙПК±
ЙПК±![]() µДЦµЈ»
µДЦµЈ»
ЈЁ3Ј©Йи![]() Ул
Ул![]()
![]() µДЦШµюІї·ЦНјРОµДГж»эОЄ
µДЦШµюІї·ЦНјРОµДГж»эОЄ![]() ЈЁЖЅ·ЅµҐО»Ј©Ј¬µ±
ЈЁЖЅ·ЅµҐО»Ј©Ј¬µ±![]() К±Ј¬Зу
К±Ј¬Зу![]() Ул
Ул![]() Ц®јдµДєЇКэ№ШПµКЅ.
Ц®јдµДєЇКэ№ШПµКЅ.
ЈЁ4Ј©µ±![]() К±Ј¬Ц±ЅУРґіц
К±Ј¬Ц±ЅУРґіц![]() ОЄµИСьИэЅЗРОК±
ОЄµИСьИэЅЗРОК±![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
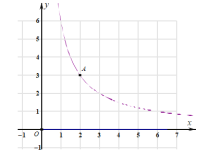
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµ xOyЦРЈ¬·ґ±ИАэєЇКэ y ![]() x 0 µДНјПуѕ№эµг A2,3 Ј¬Ц±ПЯy ax Ј¬ y
x 0 µДНјПуѕ№эµг A2,3 Ј¬Ц±ПЯy ax Ј¬ y ![]() Ул·ґ±ИАэєЇКэ y
Ул·ґ±ИАэєЇКэ y ![]() x 0 ·Ц±рЅ»УЪµг BЈ¬CБЅµгЈ®
x 0 ·Ц±рЅ»УЪµг BЈ¬CБЅµгЈ®
ЈЁ1Ј©Ц±ЅУРґіц k µДЦµ Ј»
ЈЁ2Ј©УЙПЯ¶О OBЈ¬OCєНєЇКэ y ![]() x 0 ФЪ BЈ¬C Ц®јдµДІї·ЦО§іЙµДЗшУт(І»є¬±ЯЅз)ОЄ WЈ®
x 0 ФЪ BЈ¬C Ц®јдµДІї·ЦО§іЙµДЗшУт(І»є¬±ЯЅз)ОЄ WЈ®
ўЩ µ± AµгУл BµгЦШєПК±Ј¬Ц±ЅУРґіцЗшУт W ДЪµДХыµгёцКэ Ј»
ўЪ ИфЗшУт WДЪЗЎУР 8ёцХыµгЈ¬ЅбєПєЇКэНјПуЈ¬Ц±ЅУРґіц aµДИЎЦµ·¶О§ Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄТ»ёц¶юґОєЇКэНјПуЙПІї·ЦµгµДєбЧш±к![]() УлЧЭЧш±к
УлЧЭЧш±к![]() µД¶ФУ¦ЦµИз±нЛщКѕЈє
µД¶ФУ¦ЦµИз±нЛщКѕЈє
| Ў | ©Ѓ3 | ©Ѓ2 | ©Ѓ1 | 0 | 1 | Ў |
| Ў | 0 | ©Ѓ3 | ©Ѓ4 | ©Ѓ3 | 0 | Ў |
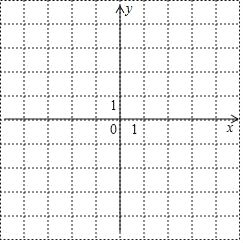
(1)ЗуХвёц¶юґОєЇКэµД±нґпКЅЈ»
(2)ФЪёш¶ЁµДЖЅГжЦ±ЅЗЧш±кПµЦР»іцХвёц¶юґОєЇКэµДНјПуЈ»
(3)µ±![]() К±Ј¬Ц±ЅУРґіц
К±Ј¬Ц±ЅУРґіц![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪ![]() µДЦ±ЅЗИэЅЗРО
µДЦ±ЅЗИэЅЗРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() КЗЦ±ЅЗ±Я
КЗЦ±ЅЗ±Я![]() ЛщФЪЦ±ПЯЙПµДТ»ёц¶ЇµгЈ¬Б¬ЅУ
ЛщФЪЦ±ПЯЙПµДТ»ёц¶ЇµгЈ¬Б¬ЅУ![]() Ј¬Ѕ«
Ј¬Ѕ«![]() ИЖµг
ИЖµг![]() ДжК±ХлРэЧЄ
ДжК±ХлРэЧЄ![]() µЅ
µЅ![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј¬
Ј¬![]() Ј®
Ј®
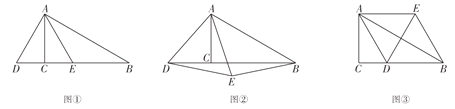
ЈЁ1Ј©ИзНјўЩЈ¬µ±µг![]() ЗЎєГФЪПЯ¶О
ЗЎєГФЪПЯ¶О![]() ЙПК±Ј¬ЗлЕР¶ППЯ¶О
ЙПК±Ј¬ЗлЕР¶ППЯ¶О![]() єН
єН![]() µДКэБї№ШПµЈ¬ІўЅбєПНјўЩЦ¤ГчДгµДЅбВЫЈ»
µДКэБї№ШПµЈ¬ІўЅбєПНјўЩЦ¤ГчДгµДЅбВЫЈ»
ЈЁ2Ј©µ±µг![]() І»ФЪЦ±ПЯ
І»ФЪЦ±ПЯ![]() ЙПК±Ј¬ИзНјўЪЎўНјўЫЈ¬ЖдЛыМхјюІ»±дЈ¬ЈЁ1Ј©ЦРЅбВЫКЗ·сіЙБўЈїИфіЙБўЈ¬ЗлЅбєПНјўЪЎўНјўЫСЎФсТ»ёцёшУиЦ¤ГчЈ»ИфІ»іЙБўЈ¬ЗлЦ±ЅУРґіцРВµДЅбВЫЈ®
ЙПК±Ј¬ИзНјўЪЎўНјўЫЈ¬ЖдЛыМхјюІ»±дЈ¬ЈЁ1Ј©ЦРЅбВЫКЗ·сіЙБўЈїИфіЙБўЈ¬ЗлЅбєПНјўЪЎўНјўЫСЎФсТ»ёцёшУиЦ¤ГчЈ»ИфІ»іЙБўЈ¬ЗлЦ±ЅУРґіцРВµДЅбВЫЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅРОABCDµД¶ФЅЗПЯACЎўBDПаЅ»УЪµгOЈ¬ЎПCABµДЖЅ·ЦПЯЅ»BDУЪµгEЈ¬Ѕ»BCУЪµгFЈ®ИфOEЈЅ2Ј¬ФтCFЈЅ_____Ј®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com