
【题目】如图,在![]() 的直角三角形
的直角三角形![]() 中,
中,![]() ,
,![]() 是直角边
是直角边![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() ,连接
,连接![]() ,
,![]() .
.
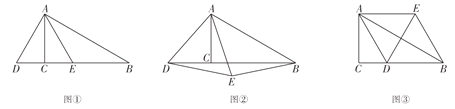
(1)如图①,当点![]() 恰好在线段
恰好在线段![]() 上时,请判断线段
上时,请判断线段![]() 和
和![]() 的数量关系,并结合图①证明你的结论;
的数量关系,并结合图①证明你的结论;
(2)当点![]() 不在直线
不在直线![]() 上时,如图②、图③,其他条件不变,(1)中结论是否成立?若成立,请结合图②、图③选择一个给予证明;若不成立,请直接写出新的结论.
上时,如图②、图③,其他条件不变,(1)中结论是否成立?若成立,请结合图②、图③选择一个给予证明;若不成立,请直接写出新的结论.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.
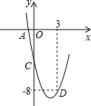
![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,经过点
,经过点![]() ,
,![]() ,
,![]() 三点.
三点.
![]() 求抛物线的解析式及顶点M的坐标;
求抛物线的解析式及顶点M的坐标;
![]() 连接AC、MB,P为线段MB上的一个动点(不与点M、B重合),过点P作x轴的垂线PQ,若OQ=a,四边形ACPQ的面积为s,求a为何值时,面积s最大;
连接AC、MB,P为线段MB上的一个动点(不与点M、B重合),过点P作x轴的垂线PQ,若OQ=a,四边形ACPQ的面积为s,求a为何值时,面积s最大;
![]() 点N是抛物线上第四象限的一个定点,坐标为
点N是抛物线上第四象限的一个定点,坐标为![]() ,过点C作直线
,过点C作直线![]() 轴,动点
轴,动点![]() 在直线l上,动点
在直线l上,动点![]() 在x轴上,连接PM、PQ、NQ,当m为何值时,
在x轴上,连接PM、PQ、NQ,当m为何值时,![]() 的和最小,并求出
的和最小,并求出![]() 和的最小值.
和的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
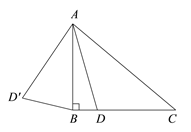
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作。《九章算术》中记载:“今有五省、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平。并燕、雀重一斤。问燕,雀一枚各重几何?”译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网上书城“五一·劳动节”期间在特定的书目中举办特价促销活动,有A、B、C、D四本书是小明比较中意的,但是他只打算选购两本,求下列事件的概率:
(1)小明购买A书,再从其余三本书中随机选一款,恰好选中C的概率是_________;
(2)小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
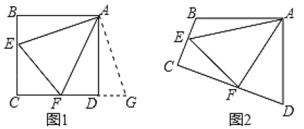
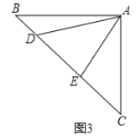
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足 关系时,线段BE、DF和EF之间依然有①中的结论存在,请你写出该结论的证明过程;
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() ,点D、E均在边BC上,且∠DAE=45°,若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°,若BD=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com