
 如图,点O是数轴的原点,点A是数轴上的一个定点,点A表示的数为-15,点B在数轴上,且OB=3OA,数轴上的两个动点M,N分别从点A和点O同时出发,向右移动,点M的运动速度为每秒3个单位,点N的运动速度为每秒2个单位.
如图,点O是数轴的原点,点A是数轴上的一个定点,点A表示的数为-15,点B在数轴上,且OB=3OA,数轴上的两个动点M,N分别从点A和点O同时出发,向右移动,点M的运动速度为每秒3个单位,点N的运动速度为每秒2个单位.分析 (1)分类讨论:点B在原点的左右两种情况下来求点P所对应的有理数;
(2)先求得点M的移动时间,然后求其移动距离;
(3)分类讨论:点B在原点的左右两种情况下,点M,N与原点的距离相等.
解答 解:(1)∵OA=15,OB=3OA,∴OB=45,
若点B在原点的右边,AB=60,
∴点B对应的有理数为45,线段AB的中点P对应的有理数为15,
若点B在原点的左边,AB=30,
∴点B对应的有理数为-45;线段AB的中点P对应的有理数为-30;
(2)当点B对应的数为正数时,则点M移动30个单位到达线段AB的中点P,点M移动的时间为$\frac{30}{3}═10$秒,此时点N移动的距离为2×10=20,
∴点N对应的有理数为20;
(3)设经过x秒点有OM=ON,
若点B在原点的右边,则3x-2x=15,x=15,
若点B在原点的左边,则15-3x=2x,x=3.
点评 本题考查了数轴和一元一次方程的应用.根据已知点运动速度以及距离之间的关系得出等式是解题关键.注意对于动点问题要分类讨论.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
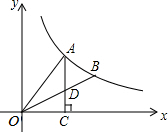 如图,A.B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为$\frac{8}{3}$.
如图,A.B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为$\frac{8}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com